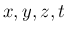 の関数であり、速度も 3 次元ベクトルであるが、
ここでは流れはほぼ
の関数であり、速度も 3 次元ベクトルであるが、
ここでは流れはほぼ 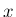 方向への 1 次元的な運動であり、
方向への 1 次元的な運動であり、
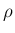 ,
, 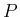 も断面に関しては一様な
も断面に関しては一様な 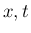 のみの関数であるとする。
のみの関数であるとする。
管内の気体は、本来は 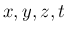 の関数であり、速度も 3 次元ベクトルであるが、
ここでは流れはほぼ
の関数であり、速度も 3 次元ベクトルであるが、
ここでは流れはほぼ 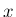 方向への 1 次元的な運動であり、
方向への 1 次元的な運動であり、
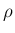 ,
, 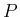 も断面に関しては一様な
も断面に関しては一様な 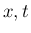 のみの関数であるとする。
のみの関数であるとする。
管内部の 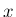 での
での 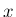 軸に垂直な断面 (
軸に垂直な断面 (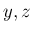 平面の領域) を
平面の領域) を 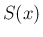 とし、
管の
とし、
管の 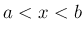 の範囲での内部 (3 次元領域) を
の範囲での内部 (3 次元領域) を 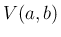 、
、
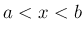 での管の壁 (
での管の壁 (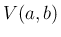 の側面側の境界の 2 次元曲面を
の側面側の境界の 2 次元曲面を 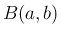 と
書くことにする。
と
書くことにする。
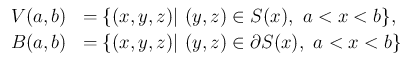
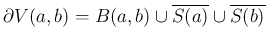 となる。
なお、
となる。
なお、
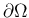 は
は 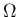 の境界を意味することとする。
の境界を意味することとする。
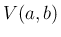 内部の気体の質量は、
内部の気体の質量は、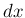 幅での微小体積
幅での微小体積 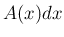 と
密度
と
密度 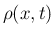 の積の積分によって得られるので、
の積の積分によって得られるので、
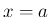 では気体は単位時間当たりに
では気体は単位時間当たりに 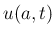 だけ右へ移動するので、
だけ右へ移動するので、
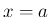 での気体の単位時間当たりの右方向への移動質量は
での気体の単位時間当たりの右方向への移動質量は
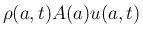
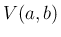 での質量 (2) の単位時間当たりの
変化は、
での質量 (2) の単位時間当たりの
変化は、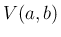 の端
の端 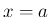 ,
, 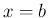 からの流入量に等しいので、
が成り立ち、この右辺は、
からの流入量に等しいので、
が成り立ち、この右辺は、
![$\displaystyle \rho(a,t)A(a)u(a,t) - \rho(b,t)A(b)u(b,t)
= -\left[\rho A(x)u\right]_a^b
= -\int_a^b(A(x)\rho u)_x\, dx
$](img34.png)
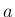 ,
, 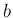 の
任意性により、被積分関数は恒等的に 0 であることになり、
よって (1) の最初の式が得られることになる。
の
任意性により、被積分関数は恒等的に 0 であることになり、
よって (1) の最初の式が得られることになる。
次は、(1) の 2 本目。
 内部の気体の運動量 (
内部の気体の運動量 ( 方向) は、
質量
方向) は、
質量 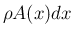 と速度
と速度 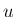 の積の積分なので、
の積の積分なので、
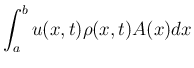
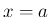 ,
, 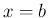 からの流入量と、
外部から
からの流入量と、
外部から 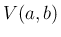 に加えられる力
に加えられる力
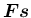 の
の  成分の和となるので、
が成り立つ。
ここで、
成分の和となるので、
が成り立つ。
ここで、
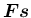 は、端
は、端 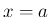 ,
, 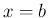 で圧力が内部を押す力の総和と、
壁
で圧力が内部を押す力の総和と、
壁 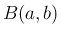 で
で 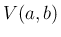 内の空気が壁を押す力の反作用の総和に等しいので、
内の空気が壁を押す力の反作用の総和に等しいので、
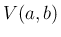 の境界
の境界
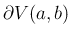 上の点における、
上の点における、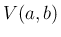 に関して
外向きの単位法線ベクトルを
に関して
外向きの単位法線ベクトルを
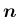 とすれば、
とすれば、
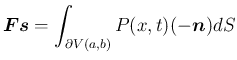
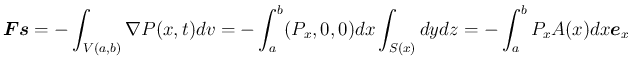
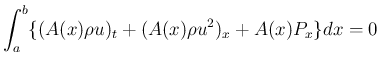
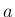 ,
, 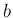 の任意性より (1) の 2 本目が得られる。
の任意性より (1) の 2 本目が得られる。
最後に (1) の 3 本目。
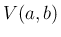 内部の気体のエネルギー総量は、質量
内部の気体のエネルギー総量は、質量 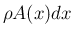 と
単位質量当たりのエネルギー
と
単位質量当たりのエネルギー 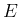 との積の積分なので、
との積の積分なので、
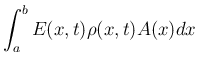
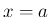 ,
, 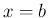 からの流入量と、端で圧力
からの流入量と、端で圧力 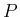 がする仕事の和になる。
管の壁
がする仕事の和になる。
管の壁 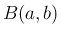 は固定壁なのでそこでの仕事はない。
よって、
は固定壁なのでそこでの仕事はない。
よって、
![$\displaystyle \frac{d}{dt}\int_a^b E\rho A(x)dx
= -\left[E\rho A(x)u\right]_a^b -\left[PA(x)u\right]_a^b
$](img50.png)
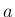 ,
,  の任意性より、(1) の 3 本目の式が
得られる。
の任意性より、(1) の 3 本目の式が
得られる。
竹野茂治@新潟工科大学