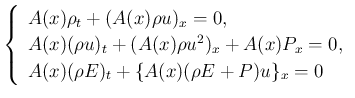 (1)
(1)
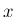 軸に沿って伸びていると考え、
軸に沿って伸びていると考え、
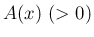 は管の
は管の 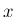 での
での 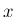 軸に垂直な断面積、
軸に垂直な断面積、
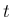 は時刻、
は時刻、
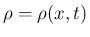 は気体密度、
は気体密度、
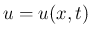 は
は 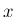 方向の気体速度、
方向の気体速度、
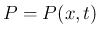 は
は 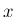 での単位面積当たりの圧力、
での単位面積当たりの圧力、
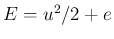 は単位質量当たりの気体のエネルギー、
は単位質量当たりの気体のエネルギー、
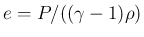 は単位質量当たりの内部エネルギー、
は単位質量当たりの内部エネルギー、
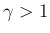 は気体定数である。
外力や粘性は本稿では考えないため省いてある。
は気体定数である。
外力や粘性は本稿では考えないため省いてある。
なお (1) は、
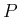 が
が 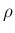 だけの関数 (
だけの関数 (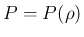 ) として、
最初の 2 本だけで考えることも良く行われている。
) として、
最初の 2 本だけで考えることも良く行われている。
この (1) は、 より一般の 3 次元的な気体運動を表す圧縮性オイラー方程式を 導くのと同様、積分形の保存則に戻って、そこから微分方程式を導く方法を 取っていることが多いように思う (例えば [1], [3], [4])。
しかし、3 次元オイラー方程式を導く際にすでにその方法、 すなわち積分形の保存則から微分方程式を導く方法を 用いているのであるから、 積分形の保存則を経由せずに 3 次元オイラー方程式から直接 (1) を導くこともできそうな気がする。 本稿は、それについて考察することが目標である。
竹野茂治@新潟工科大学