6.3 1 次因数を持つかどうかの判別
最後に、
![$\displaystyle f(x)=\sum_{j=0}^n a_jx^j\in\mathbb{Z}[x]$](img214.gif) (
(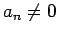 ,
, 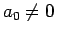 ) が有理数の範囲で 1 次因数を
持つかどうかの判別について説明する。
) が有理数の範囲で 1 次因数を
持つかどうかの判別について説明する。
有理数の範囲で 1 次因数を持てば、補題 5 により
それは整数の範囲でも 1 次因数を持つことになる。
その因数を 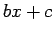 とすると、
とすると、
となるから、その最高次の係数と最低次の係数を比較すれば、
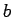 は
は 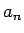 の約数、
の約数、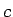 の絶対値は
の絶対値は 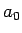 の約数であることがわかる。
よって、その組み合わせは
の約数であることがわかる。
よって、その組み合わせは 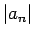 の約数の個数
の約数の個数 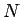 と、
と、
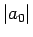 の約数の個数
の約数の個数 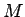 の 2 倍 (
の 2 倍 (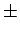 の符号の分) だけあり、
すなわち
の符号の分) だけあり、
すなわち 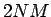 通りになる。それらが実際に因数であるかは、
因数定理により
通りになる。それらが実際に因数であるかは、
因数定理により 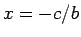 を
を 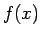 に代入して 0 になるかを
確認すればよいので、それで確実に 1 次因数の存在が判別できることになる。
に代入して 0 になるかを
確認すればよいので、それで確実に 1 次因数の存在が判別できることになる。
3 次式の場合には、それが有理数の範囲で因数分解できれば、
必ず有理数係数の 1 次因数があることになるので、
3 次式が有理数の範囲で因数分解できるかどうかは
有限回の手続きで容易に確認できることになる。
竹野茂治@新潟工科大学
2018-03-02
![$\displaystyle f(x)=\sum_{j=0}^n a_jx^j\in\mathbb{Z}[x]$](img214.gif)
![$\displaystyle f(x)=\sum_{j=0}^n a_jx^j\in\mathbb{Z}[x]$](img214.gif) (
(![]() とすると、
とすると、