6 一般の μ の場合
それでは、一般の 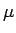 の場合はどうなるのかを次に考えてみることにする。
の場合はどうなるのかを次に考えてみることにする。
5 節の 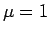 の場合の議論を見れば、
の場合の議論を見れば、
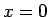 での境界条件の不要性は、
結局
での境界条件の不要性は、
結局 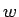 の
の 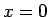 での有界性から (20) の
での有界性から (20) の 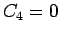 が
導かれることに起因することがわかる。
よって、一般の
が
導かれることに起因することがわかる。
よって、一般の 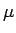 の場合にも 3 節、5 節と同様の変数分離法を用いて、
の場合にも 3 節、5 節と同様の変数分離法を用いて、
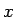 に関する方程式をベッセルの方程式に帰着させることで考察してみることにする。
に関する方程式をベッセルの方程式に帰着させることで考察してみることにする。
方程式 (5) に対して 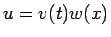 とすると、
とすると、
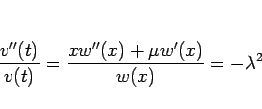
となるので、
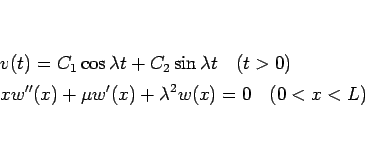
となる。
5 節と同様に 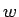 を (18) のように置いて変形すると、この場合は
を (18) のように置いて変形すると、この場合は
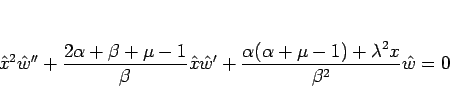 |
(26) |
となるので、よって
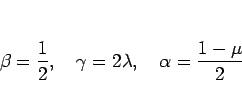
とすることで
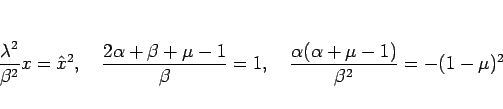
となって、よって (26) は
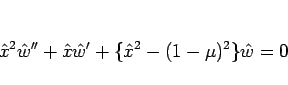
の形、すなわち 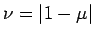 のベッセルの微分方程式となる。
のベッセルの微分方程式となる。
まず 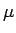 が整数でない場合は、
が整数でない場合は、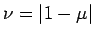 も整数ではなく、
よって
も整数ではなく、
よって 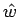 は
は
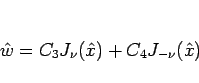
と書けるので、これにより 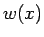 は
は
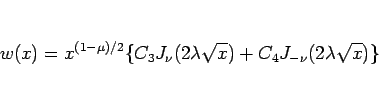 |
(27) |
となるが、(13) より
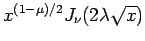 は
は
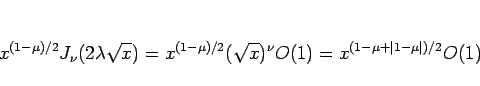
となるので、これはどんな 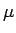 に対しても
に対しても 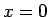 の近くで有界となる。
一方、(14) より
の近くで有界となる。
一方、(14) より
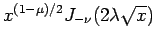 は
は
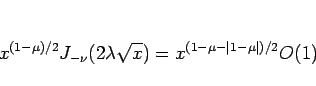
となるので、これは 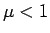 ならば有界であるが、
ならば有界であるが、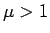 ならば有界ではない。
つまり、
ならば有界ではない。
つまり、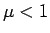 ならば (27) の
ならば (27) の 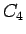 は残るが、
は残るが、
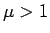 ならば
ならば 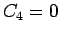 ではなくてはならないことになる。
ではなくてはならないことになる。
次に 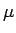 が整数の場合は、
が整数の場合は、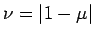 も整数なので、
も整数なので、
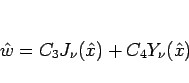
より、
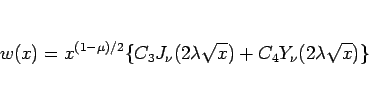 |
(28) |
となる。
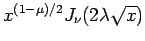 は
は 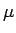 が整数でない場合と同様に
が整数でない場合と同様に 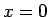 で常に有界であるが、
で常に有界であるが、
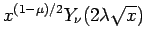 は (15) より、
は (15) より、
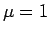 のときは
のときは
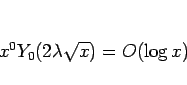
より有界ではなく、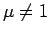 のときは、
のときは、
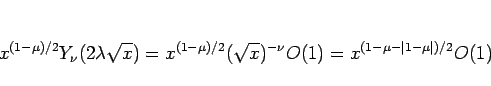
となるので、やはり 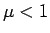 ならば有界、
ならば有界、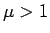 ならば有界ではない。
よって、
ならば有界ではない。
よって、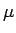 が整数の場合も
が整数の場合も 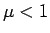 ならば
ならば 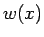 は有界なので (28) の
は有界なので (28) の 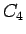 は残るが、
は残るが、
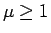 ならば有界ではないので
ならば有界ではないので 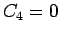 でなくてはならない。
でなくてはならない。
結局以上をまとめると、以下のようになる。
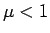 の場合は、(27), (28) の
の場合は、(27), (28) の 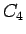 が残るので、それを決定するために
が残るので、それを決定するために 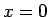 での境界条件 (6) が必要
での境界条件 (6) が必要
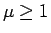 の場合は、(27), (28) の
の場合は、(27), (28) の 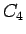 は、
は、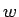 が有界であるためには 0 ではなくてはならず、
よって
が有界であるためには 0 ではなくてはならず、
よって 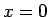 での境界条件 (6) は不要
での境界条件 (6) は不要
竹野茂治@新潟工科大学
2009年6月22日
![]() の場合の議論を見れば、
の場合の議論を見れば、
![]() での境界条件の不要性は、
結局
での境界条件の不要性は、
結局 ![]() の
の ![]() での有界性から (20) の
での有界性から (20) の ![]() が
導かれることに起因することがわかる。
よって、一般の
が
導かれることに起因することがわかる。
よって、一般の ![]() の場合にも 3 節、5 節と同様の変数分離法を用いて、
の場合にも 3 節、5 節と同様の変数分離法を用いて、
![]() に関する方程式をベッセルの方程式に帰着させることで考察してみることにする。
に関する方程式をベッセルの方程式に帰着させることで考察してみることにする。
![]() とすると、
とすると、
![]() が整数でない場合は、
が整数でない場合は、![]() も整数ではなく、
よって
も整数ではなく、
よって ![]() は
は
![]() が整数の場合は、
が整数の場合は、![]() も整数なので、
も整数なので、