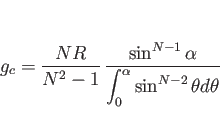8 最後に
本稿では、[1] に続いて軸対称の曲面と
立体の重心の計算について考察した。特に新しい知見があるわけではないが、
円、球に関する例の場合、2 次元図形と 3 次元図形で式に違いがあることに
少し興味を感じた。
これは、実は次元に由来していて、例えば 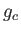 は、一般の
は、一般の 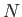 次元では、
次元では、
となる。この分母の積分は、部分積分すればわかるが、
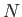 が偶数か奇数かによって結果が変わり、偶数の場合には
が偶数か奇数かによって結果が変わり、偶数の場合には 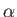 が
直接現れ、奇数次元の場合は
が
直接現れ、奇数次元の場合は 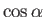 のみで表される式となる。
のみで表される式となる。
竹野茂治@新潟工科大学
2019-03-05
![]() は、一般の
は、一般の ![]() 次元では、
次元では、