7 対称性
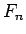 は、A, B のどちらが上であるかを考えないゲーム差の平均値であるから、
互角のところ (
は、A, B のどちらが上であるかを考えないゲーム差の平均値であるから、
互角のところ (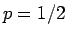 ) で対称になっていて、
またその互角のところではゲーム差が 0 に近いことが期待されるので、
) で対称になっていて、
またその互角のところではゲーム差が 0 に近いことが期待されるので、
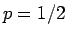 で最小値を取ることが予想される。
この節ではそれを考えてみる。
すなわち、以下の 2 つを示す。
で最小値を取ることが予想される。
この節ではそれを考えてみる。
すなわち、以下の 2 つを示す。
-
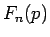 は
は 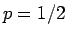 に関して対称、すなわち
に関して対称、すなわち
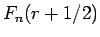 は
は 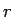 に関して偶関数となる
に関して偶関数となる
-
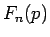 は
は
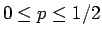 では減少、
では減少、
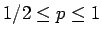 では増加する。
よって
では増加する。
よって 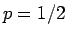 で最小値を取り、
で最小値を取り、
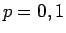 で最大値
で最大値 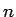 を取る
を取る
最後の最大値 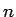 は、
は、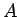 が必ず勝つのであれば当然ゲーム差は
が必ず勝つのであれば当然ゲーム差は 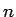 となるだろう。
となるだろう。
5 節の (14) より、
これはいずれも 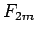 について考えればよいことがわかる。
ここでは (15) を用いて考えることにする。
について考えればよいことがわかる。
ここでは (15) を用いて考えることにする。
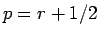 とすると
とすると 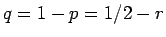 であるから、
であるから、
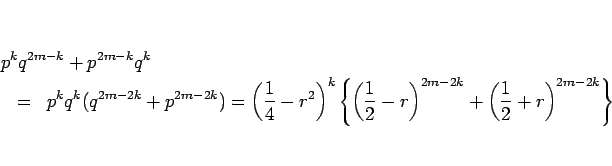
となるので、これは明らかに 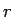 の偶関数となる (
の偶関数となる (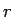 の代わりに
の代わりに 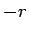 を代入しても不変)。
よって (15) より
を代入しても不変)。
よって (15) より 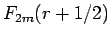 は確かに
は確かに 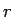 の偶関数となる。
の偶関数となる。
次に (15) を 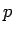 の式とみて
の式とみて 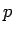 で微分する。
で微分する。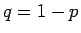 より
より
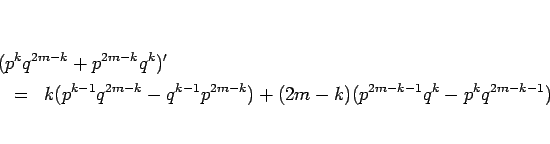
となるが、今
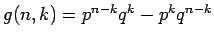 と書くことにすると、これは
と書くことにすると、これは
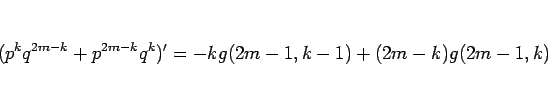
と書ける。
よって、(15) より、
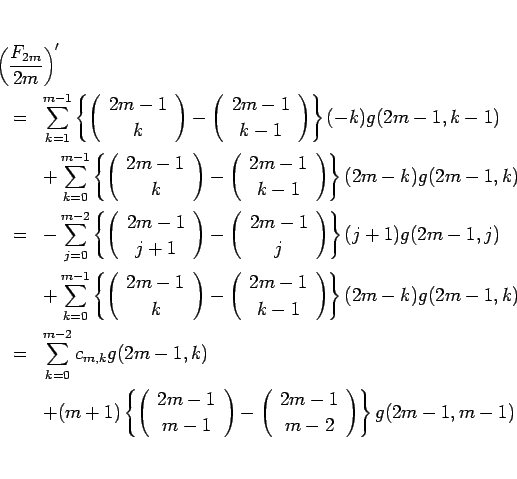
と変形すると、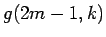 の係数
の係数 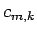 は 5 節と同様の変形により、
は 5 節と同様の変形により、
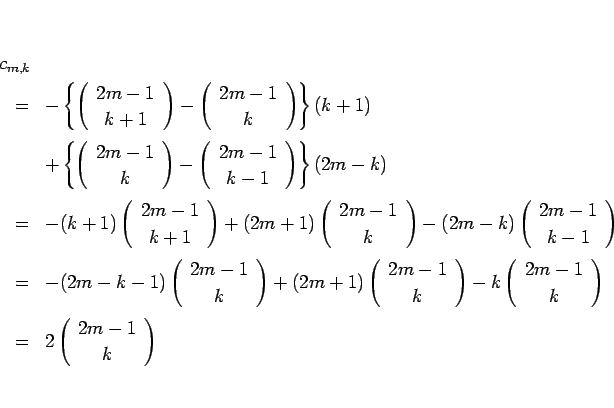
と書き直せる。同様に、
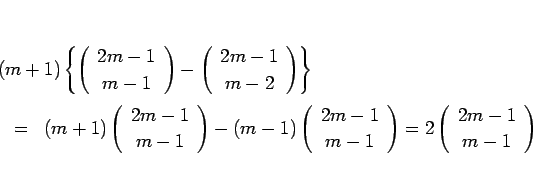
となるので、結局
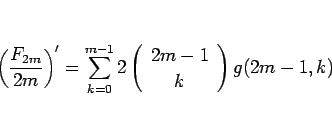
となる。ここで、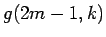 は
は
 に対し、
に対し、
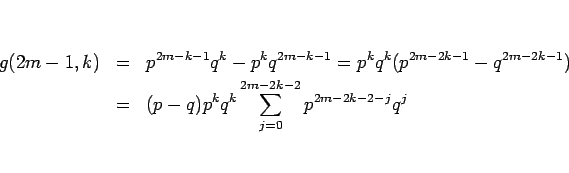
と因数分解され、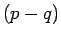 以外の部分は
以外の部分は 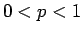 では正であり、
では正であり、
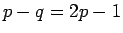 は
は 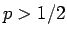 で正、
で正、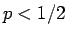 で負なので、
この節最初の主張の 2. の増減の部分が言えたことになる。
で負なので、
この節最初の主張の 2. の増減の部分が言えたことになる。
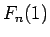 の値は、例えば (6) に
の値は、例えば (6) に 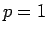 ,
, 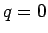 を代入すれば
を代入すれば
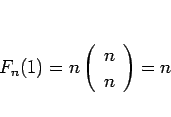
となる。
竹野茂治@新潟工科大学
2009年7月27日
![]() について考えればよいことがわかる。
ここでは (15) を用いて考えることにする。
について考えればよいことがわかる。
ここでは (15) を用いて考えることにする。
![]() とすると
とすると ![]() であるから、
であるから、
![]() の式とみて
の式とみて ![]() で微分する。
で微分する。![]() より
より
![]() の値は、例えば (6) に
の値は、例えば (6) に ![]() ,
, ![]() を代入すれば
を代入すれば