5 一般の場合
次に、一般の 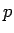 の場合の
の場合の 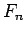 について考える。
これも、最初のいくつかを計算してみよう。
について考える。
これも、最初のいくつかを計算してみよう。
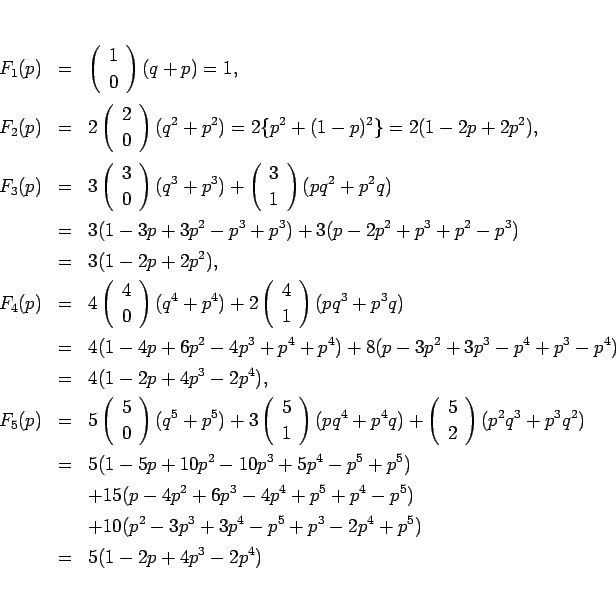
ここから、(12) を拡張した、
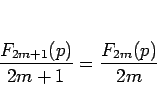 |
(14) |
が成り立つことが予想される。本節ではこれを示す。
(7), (8) に共通の係数の部分は、
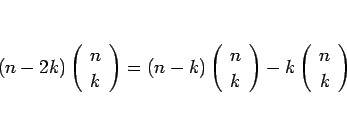
と分けると、
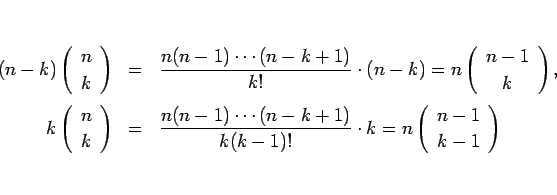
と変形できるから、
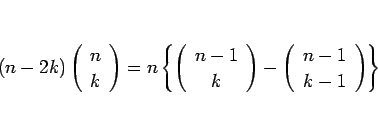
となり、よって、(7), (8) は
となる。この両者の右辺が等しくなることを示す。
まず、
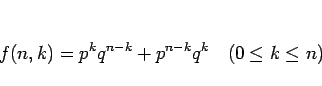 |
(17) |
と書くことにすると、(16) の和の中の 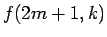 の
の
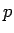 の最高次の項は、
の最高次の項は、
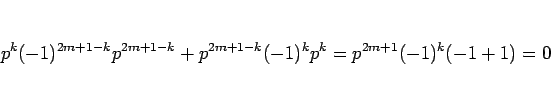
となって、実際には次数が 1 つ下がることになる。
よって、これを 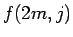 で表すことを考えてみる。
で表すことを考えてみる。
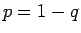 ,
, 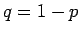 なので、
なので、
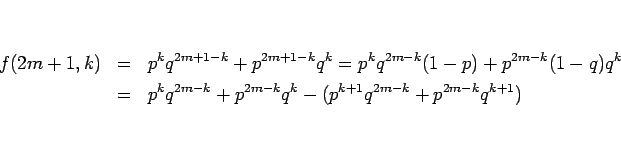
となるので、
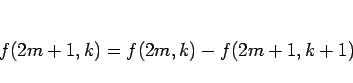
が成り立つことになる。これを繰り返し用いると、
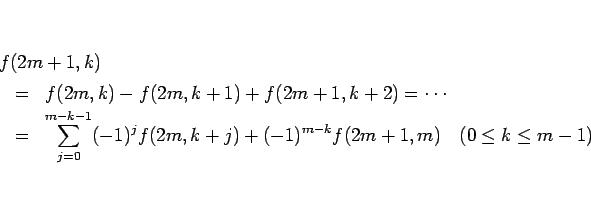
となるので、これを (16) に代入すると、
となる。ここで二重和が出てきたが、以下では二重和の交換定理
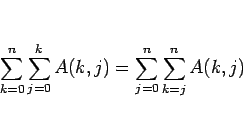 |
(20) |
を何度か用いる。
今、(19) の二重和の項の方で 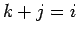 とすると、
(20) より
とすると、
(20) より
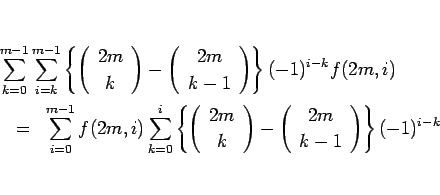
となるので、
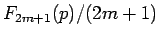 は、
は、
と書けることになる。よってあとはこの係数部分の
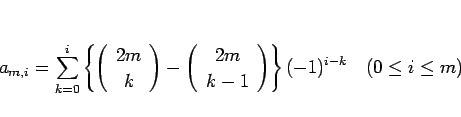 |
(22) |
を考えればよい。これに (13) を用いると、
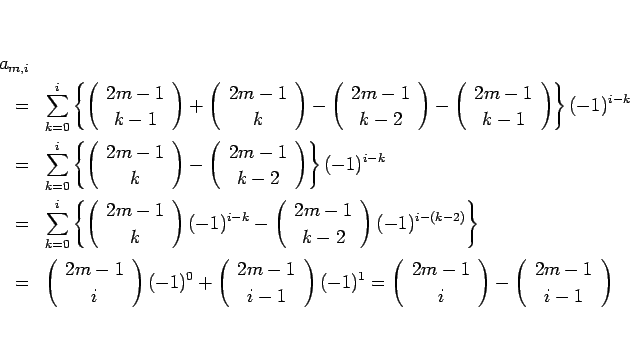
となることがわかる。特に、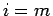 の場合は、
の場合は、
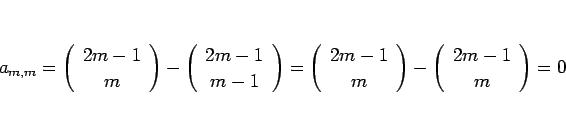
となるので、結局 (21) は、
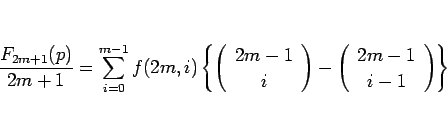
となり、(15) よりこれは
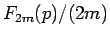 に等しいことがわかる。
に等しいことがわかる。
竹野茂治@新潟工科大学
2009年7月27日
![]() とすると、
(20) より
とすると、
(20) より