4 互角の場合の符号無しゲーム差の平均
次に 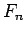 の方を考える。こちらは
の方を考える。こちらは 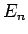 に比べてかなり厄介である。
(4) と同様に、
に比べてかなり厄介である。
(4) と同様に、
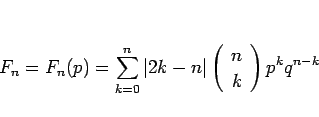 |
(6) |
であるが、絶対値を外すために、
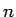 が偶数の場合と奇数の場合に分けて考えることにする。
まず、
が偶数の場合と奇数の場合に分けて考えることにする。
まず、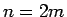 の場合は、
の場合は、
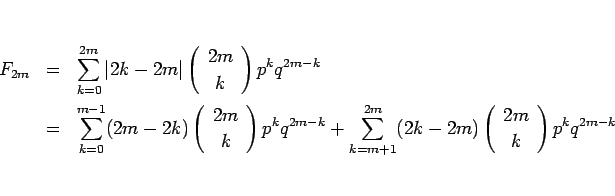
となるが、この後ろの和で 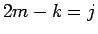 とすると
とすると
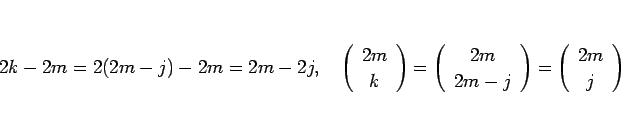
なので、
同様に、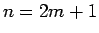 の場合は、
の場合は、
となる。例えば、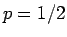 のときは、
のときは、
となるが、いくつか計算してみると、
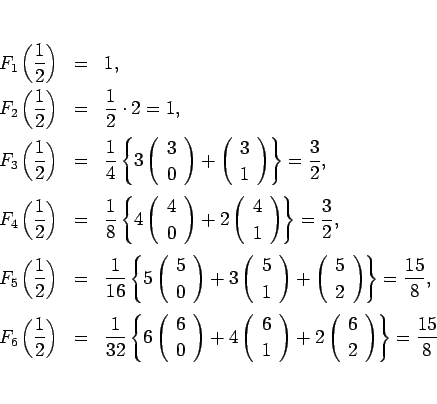
のようになることがわかる。実は一般に次が言える。
(12) は、5 節で
より一般のものを示すから、ここでは (11) を示そう。
そのために、二項係数に成り立つ次の関係式を用いる。
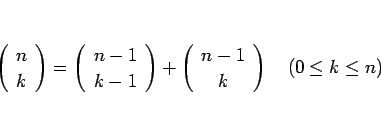 |
(13) |
ただし、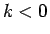 および
および 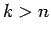 のときは
のときは
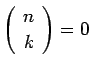 とする。
これは、二項係数に関するパスカルの三角形の元となる関係式である。
とする。
これは、二項係数に関するパスカルの三角形の元となる関係式である。
(9) にこの (13) を用いると、
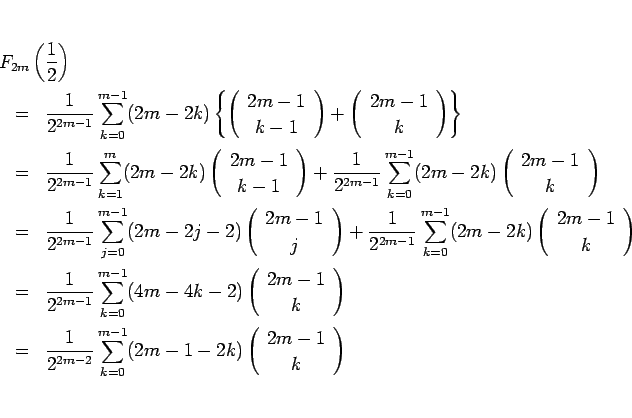
となり、これは (10) により 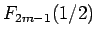 に等しいから (11) が言えたことになる。
に等しいから (11) が言えたことになる。
竹野茂治@新潟工科大学
2009年7月27日
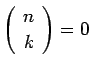 とする。
これは、二項係数に関するパスカルの三角形の元となる関係式である。
とする。
これは、二項係数に関するパスカルの三角形の元となる関係式である。