6 展開式への変形
5 節では、
最初にいくつかの 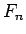 を
を 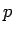 の式として展開したが、
考察は
の式として展開したが、
考察は 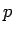 ,
, 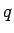 の式のままでの計算を行った。
この節では、その
の式のままでの計算を行った。
この節では、その 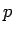 の式としての展開式の計算を行ってみることにする。
の式としての展開式の計算を行ってみることにする。
5 節では、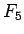 まで計算したが、
実際には (14) より偶数次の方のみを考えればよい。
まで計算したが、
実際には (14) より偶数次の方のみを考えればよい。
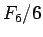 の展開を (15) により行ってみると、
の展開を (15) により行ってみると、
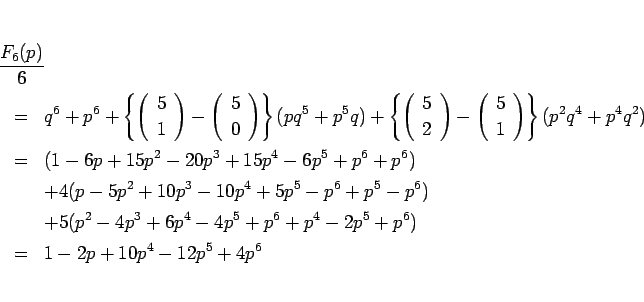
のようになる。5 節の 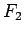 ,
, 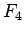 とこの
とこの 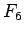 を見ると、
を見ると、
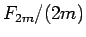 はいずれも、
はいずれも、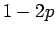 で始まり、
で始まり、
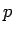 の 2 次から
の 2 次から 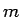 次までの項がすべて消えている。
これが一般に言えるかどうかを考えてみよう。
次までの項がすべて消えている。
これが一般に言えるかどうかを考えてみよう。
(15) に 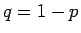 を代入して
二項定理 (5) で展開すると、
を代入して
二項定理 (5) で展開すると、
となる。この前半の和に対して 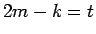 とすると、その和は
とすると、その和は
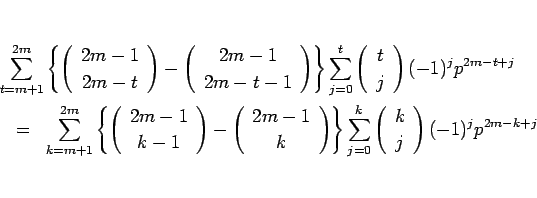
となるので、
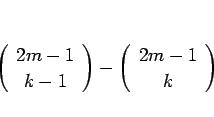
が 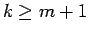 では正、
では正、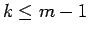 では負、
では負、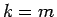 では 0 となることを考えると、
(23) は結局
では 0 となることを考えると、
(23) は結局
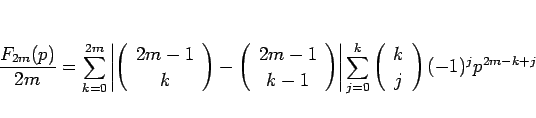
と書けることがわかる。この式で 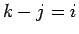 とし、和の順序交換を行えば、
とし、和の順序交換を行えば、
となる。この内側の和を 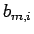 とおく:
とおく:
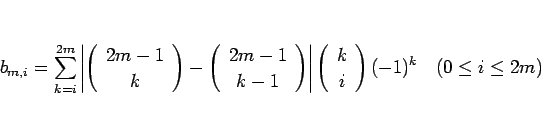 |
(25) |
まず、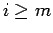 の場合を考えると、それはこの節最初の例による考察から、
の場合を考えると、それはこの節最初の例による考察から、
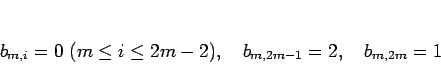 |
(26) |
であることが予想される。
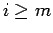 の場合は、
の場合は、
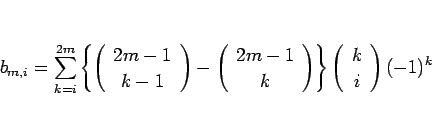
であるが、今、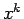 の
の 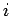 階微分を考えると
階微分を考えると
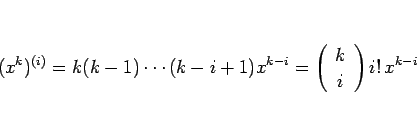
より
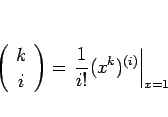
と見ることができるので、
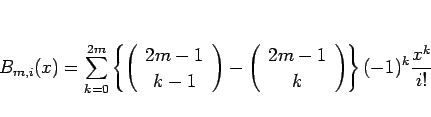 |
(27) |
とすると
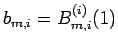 となることがわかる (
となることがわかる (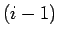 次以下の項の
次以下の項の 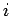 階微分は 0 となる)。
階微分は 0 となる)。
一方で、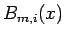 は、
は、
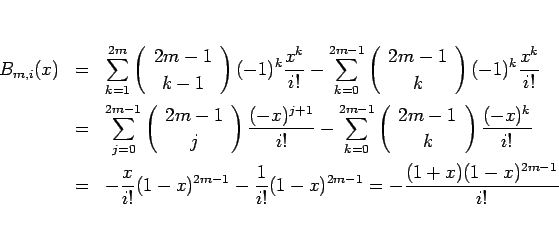
であるから、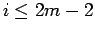 であれば
であれば 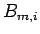 の
の 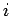 階微分には必ず
階微分には必ず
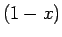 がすべての項に残るので、
がすべての項に残るので、
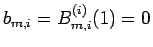 となることがわかる。
となることがわかる。
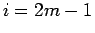 のときは、
のときは、
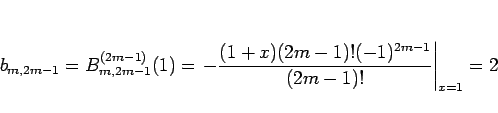
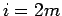 のときは、
のときは、
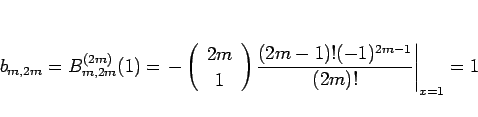
となって、(26) が確かに言えたことになる。
次に、
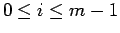 の場合を考える。この場合は、
の場合を考える。この場合は、
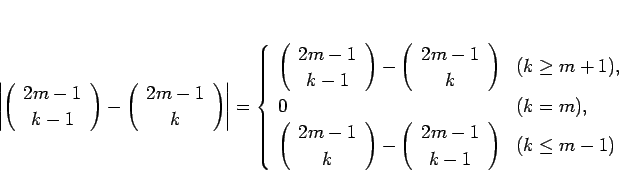
であるから、
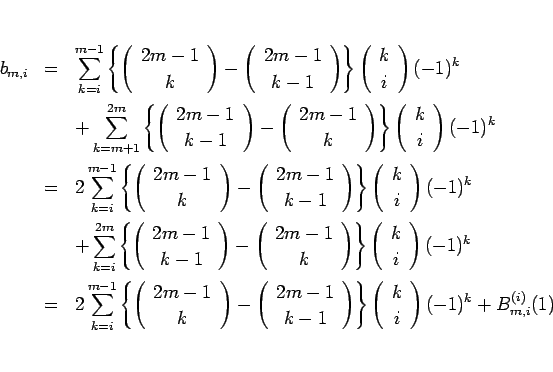
となり、この最後の項は 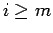 の場合と同様に 0 となるから結局
の場合と同様に 0 となるから結局
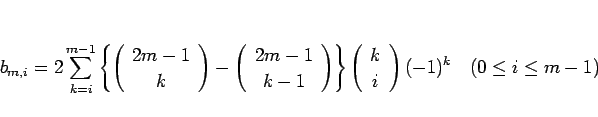
となる。これと (26) を (24) に代入すれば
| 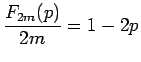 |
| |
|
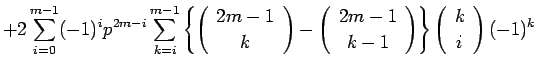 |
(28) |
となる。この式の二重和の順序を入れかえると、その和の部分は
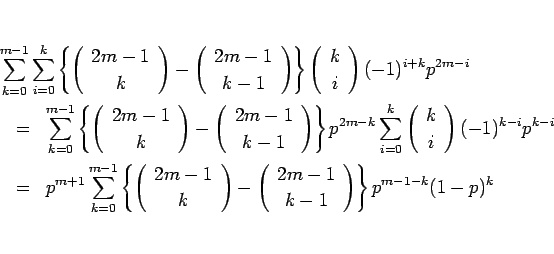
となり、結局、
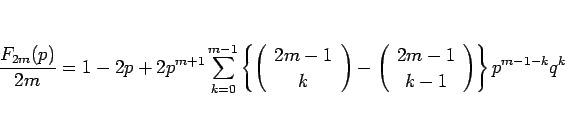 |
(29) |
のように書けることになる。
例えば、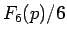 は、この式を使えば、
は、この式を使えば、
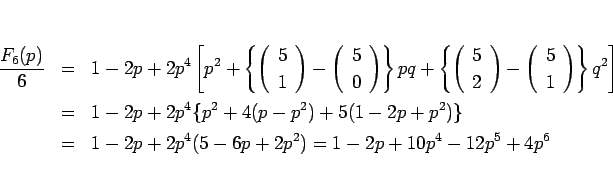
となり、この節の最初の計算よりだいぶ楽であることがわかる。
竹野茂治@新潟工科大学
2009年7月27日
![]() まで計算したが、
実際には (14) より偶数次の方のみを考えればよい。
まで計算したが、
実際には (14) より偶数次の方のみを考えればよい。
![]() の展開を (15) により行ってみると、
の展開を (15) により行ってみると、
![]() の場合は、
の場合は、
![]() は、
は、
![]() のときは、
のときは、
![]() の場合を考える。この場合は、
の場合を考える。この場合は、
![]() は、この式を使えば、
は、この式を使えば、