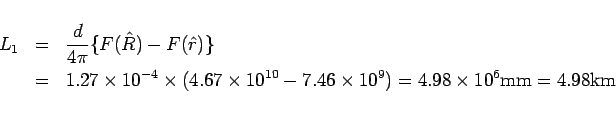次へ: 6 数値計算の際の注意
上へ: CD の溝の長さについて
前へ: 4 曲線の長さの公式の説明
(PDF ファイル: cd1.pdf)
5 数値計算
式 (1) と式 (4) とでは
かなり見た目に違いがありますが、
実際どれくらい違うのか数値計算してみました。
まず、式 (1) の 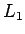 と式 (4) の
と式 (4) の 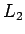 は、
は、
とすると、それぞれ
と書けます。
よって、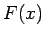 と
と 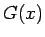 が近ければ、
この
が近ければ、
この 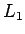 と
と 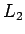 両者の値も近くなりますが、
両者の値も近くなりますが、
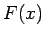 ,
, 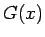 のグラフを並べて書いてみると
図 2, 3 のようになります。
のグラフを並べて書いてみると
図 2, 3 のようになります。
図 2:
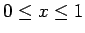 のグラフ
のグラフ
|
|
図 3:
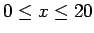 のグラフ
のグラフ
|
|
見てわかる通り、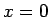 の近くでは多少違いがあるようですが、
大きい
の近くでは多少違いがあるようですが、
大きい 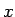 に対しては、
に対しては、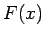 や
や 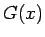 の値に比べて
その違いはごく小さなものになります。
の値に比べて
その違いはごく小さなものになります。
実際に計算してみるとわかりますが、
なので、
より、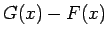 は
は 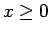 で常に 0 以上で、
かつ増加する関数ですが、
で常に 0 以上で、
かつ増加する関数ですが、
のようにその増加は非常にゆっくりです。
実際の CD の場合、
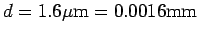 のようで、
のようで、
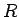 ,
, 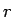 は簡単に測ってみたところ、
は簡単に測ってみたところ、
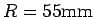 ,
,
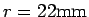 くらいのようですから、
くらいのようですから、
として計算してみると、
というごく小さい値になります。
なお、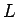 自体の長さは、
自体の長さは、
となります。
よって、(1) と (4) は CD の場合は非常に近い、
と言えるのではないかと思います。
次へ: 6 数値計算の際の注意
上へ: CD の溝の長さについて
前へ: 4 曲線の長さの公式の説明
竹野茂治@新潟工科大学
2005年9月23日
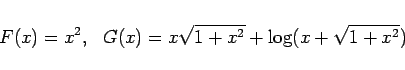
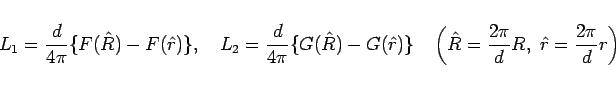
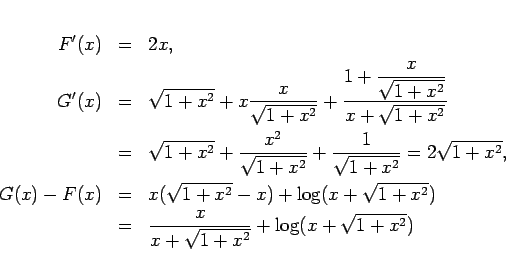
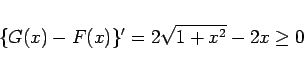
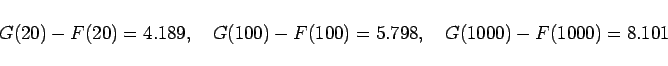
![]() のようで、
のようで、
![]() ,
, ![]() は簡単に測ってみたところ、
は簡単に測ってみたところ、
![]() ,
,
![]() くらいのようですから、
くらいのようですから、
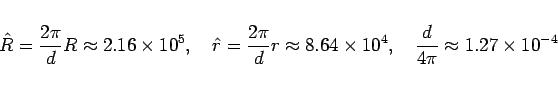
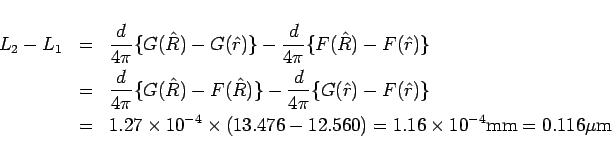
![]() 自体の長さは、
自体の長さは、