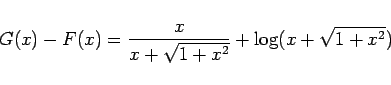
5 節でも桁落ちが起こらない、引き算を整理した式
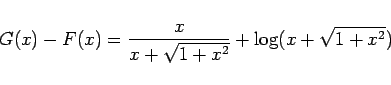
電卓を使ってみればわかりますが、
例えば
![]() のときに
のときに ![]() を計算するのは
あまり得ではなくて、代わりに
を計算するのは
あまり得ではなくて、代わりに ![]() を使えば十分です。
つまり、実際には数式をそのまま計算に使用しているのでなく、
必要な桁数を考えながら近似式を使って計算しています。
を使えば十分です。
つまり、実際には数式をそのまま計算に使用しているのでなく、
必要な桁数を考えながら近似式を使って計算しています。
この節では、![]() が大きな
が大きな ![]() に対して
どのような近似式で近似できるかを考えてみます。
に対して
どのような近似式で近似できるかを考えてみます。
![]() が小さければテイラー展開で済みますが、
今回は
が小さければテイラー展開で済みますが、
今回は ![]() は大きな値なのでそうはいきません。
は大きな値なのでそうはいきません。
まず、![]() の後ろの対数の項ですが、
の後ろの対数の項ですが、
![]() と思えば
と思えば
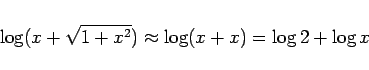
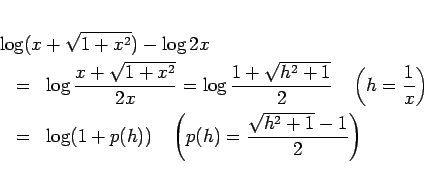
良く知られているように ![]() が小さいときは
が小さいときは
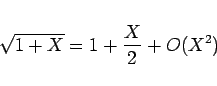
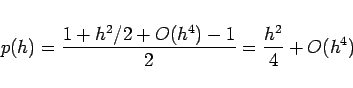
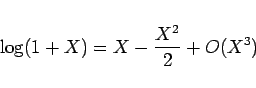
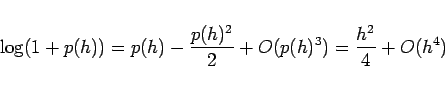
今度は ![]() の最初の項ですが、
これも
の最初の項ですが、
これも
![]() と思えば、
と思えば、
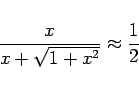
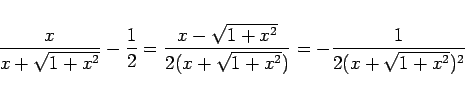
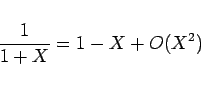
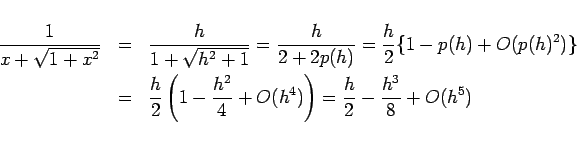
このような、大きな ![]() に対する関数の展開式を「漸近展開」と呼びます。
実は 5 節の最後の計算ではこの式を用いて
(
に対する関数の展開式を「漸近展開」と呼びます。
実は 5 節の最後の計算ではこの式を用いて
(![]() 以降の項を無視して)、
以降の項を無視して)、
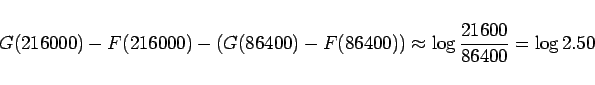
![]() のような大きな値の場合、
のような大きな値の場合、![]() は
は
![]() 程度の小さな値になりますからこれで問題はありません。
程度の小さな値になりますからこれで問題はありません。
数値計算や数式の様子を調べる現場では、テイラー展開だけではなくて、 このような漸近展開も広く使われています。