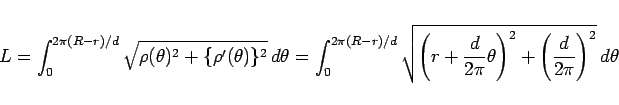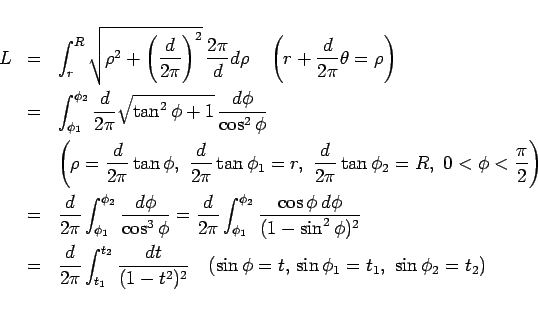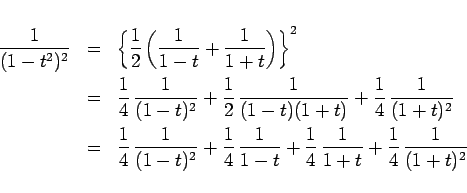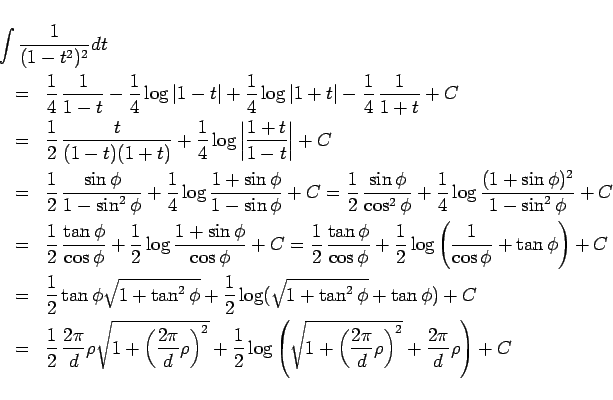次へ: 4 曲線の長さの公式の説明
上へ: CD の溝の長さについて
前へ: 2 面積による考え方
(PDF ファイル: cd1.pdf)
3 らせんの弧長
溝は円のように回っていますが、実際には少しずつ半径が変化していて、
一周すると 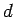 だけずれることになります。
だけずれることになります。
最も内側からスタートするとして中心からの距離 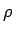 と回転角
と回転角 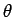 の関係を考えてみます。
角度の増加に対し均等に中心からの距離が増えると仮定すると、
の関係を考えてみます。
角度の増加に対し均等に中心からの距離が増えると仮定すると、
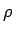 は回転角
は回転角 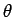 の一次式で表わされます。
一周で
の一次式で表わされます。
一周で 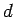 だけ増えるわけですから、
単位角度 (1 ラジアン) 辺りの
だけ増えるわけですから、
単位角度 (1 ラジアン) 辺りの 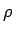 の増加は
の増加は 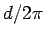 となります。
よって、
となります。
よって、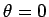 のとき
のとき 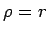 とすれば
とすれば 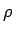 は
は
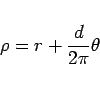 |
(2) |
という式で表わされることになります。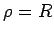 のときの
のときの 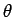 は
は
より、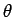 の動く範囲は
の動く範囲は
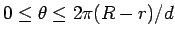 となります。
となります。
一般に曲線上の点が
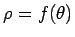 で表わされているとき、
で表わされているとき、
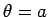 から
から 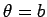 の範囲の曲線の長さ
の範囲の曲線の長さ 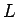 は次の式で求められます。
は次の式で求められます。
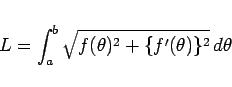 |
(3) |
この公式の説明は 4 節で行ないます。
この公式より、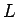 は以下のようになります。
は以下のようになります。
この式を置換積分で変形していきます。
ここで、
なので、
となります。結局、
となることがわかります。
この式の最後の右辺を 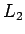 とします。
とします。
次へ: 4 曲線の長さの公式の説明
上へ: CD の溝の長さについて
前へ: 2 面積による考え方
竹野茂治@新潟工科大学
2005年9月23日
![]() と回転角
と回転角 ![]() の関係を考えてみます。
角度の増加に対し均等に中心からの距離が増えると仮定すると、
の関係を考えてみます。
角度の増加に対し均等に中心からの距離が増えると仮定すると、
![]() は回転角
は回転角 ![]() の一次式で表わされます。
一周で
の一次式で表わされます。
一周で ![]() だけ増えるわけですから、
単位角度 (1 ラジアン) 辺りの
だけ増えるわけですから、
単位角度 (1 ラジアン) 辺りの ![]() の増加は
の増加は ![]() となります。
よって、
となります。
よって、![]() のとき
のとき ![]() とすれば
とすれば ![]() は
は
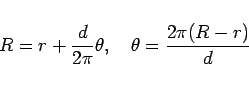
![]() で表わされているとき、
で表わされているとき、
![]() から
から ![]() の範囲の曲線の長さ
の範囲の曲線の長さ ![]() は次の式で求められます。
は次の式で求められます。