次へ: 3 らせんの弧長
上へ: CD の溝の長さについて
前へ: 1 はじめに
(PDF ファイル: cd1.pdf)
2 面積による考え方
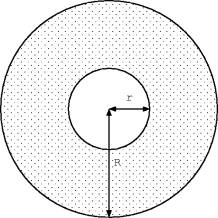
溝の間隔を 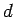 として、CD の内径を
として、CD の内径を 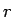 、外径を
、外径を 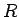 、
溝の総延長を
、
溝の総延長を 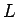 とします (図 1)。
とします (図 1)。
CD の溝のある部分の面積は、半径 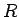 の円の面積から半径
の円の面積から半径 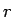 の円の面積を
引けば得られるので
の円の面積を
引けば得られるので 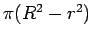 です。
です。
一方、溝を真っ直ぐに伸ばすと、長さ 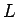 、幅
、幅 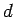 の細長い長方形ができますから
面積は
の細長い長方形ができますから
面積は 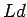 、よって、
、よって、
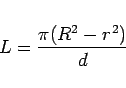 |
(1) |
となります。この式の右辺を 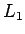 とします。
とします。
次へ: 3 らせんの弧長
上へ: CD の溝の長さについて
前へ: 1 はじめに
竹野茂治@新潟工科大学
2005年9月23日
![]() の円の面積から半径
の円の面積から半径 ![]() の円の面積を
引けば得られるので
の円の面積を
引けば得られるので ![]() です。
です。
![]() 、幅
、幅 ![]() の細長い長方形ができますから
面積は
の細長い長方形ができますから
面積は ![]() 、よって、
、よって、