まず白夜の方であるが、
太陽は
![]() に垂直な面上で、中心
に垂直な面上で、中心
![]() の円運動であり、
その最下点を H とする (図 8) と、
の円運動であり、
その最下点を H とする (図 8) と、
となることがわかる。 よって、このベクトルの
=
+
= -
sin
sin
- R
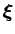
| = | - |
||
| = | - 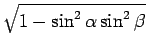 cos cos |
が条件となる。これは sin
-sinsin
tan
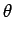
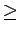
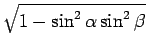
| sin2 |
|||
| sin2 |
|||
| sin2 |
のときに白夜となることがわかる。なお、これは
-sin 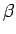
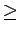
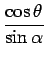
(11)
でなければ起こり得ず、逆にこのときはそのような季節が存在する。 そしてこの不等式は、
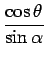
1
より、
cos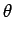
sin
= cos
-
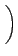
となる。よってこの (12) を満たす高緯度地帯で、 (11) が満たされる季節が白夜、ということになる。
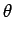
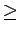
-
= 90o -23.44o = 66.56o
(12)
次に、太陽が真上に来るのはどういう場所であるかを考えてみる。
これは、図 8 の軌道最上点 K 以外は、
![]() は
は
![]() 成分を持つので真上にはこず、
(10) より
成分を持つので真上にはこず、
(10) より
となり、このベクトルの
=
+
= -
sin
sin
+ R
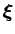
| = | - |
||
| = | - 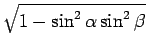 sin sin |
という場合になる。これは sin
-sinsin
=
tan
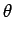
| sin2 |
|||
| sin2 |
|||
| sin2 |
のとき、ということがわかる。なお、これは
-sin =
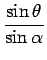
(13)
でなければこれは起こり得ず、逆にこのときはそのような季節が存在する。 そしてこの不等式は、
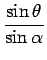
1
を意味する。この緯度 23.44o は 北回帰線 と呼ばれている。 よって、この北回帰線を越えて赤道に近い方にいけば、 (13) を満たす日には 太陽を真上に見ることができることになる。
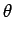
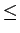
= 23.44o
(14)
竹野茂治@新潟工科大学