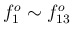 を、
各 10 秒位演奏し、その各音源から出だし付近を除いた
安定している 3 秒程度の部分を使用した。
を、
各 10 秒位演奏し、その各音源から出だし付近を除いた
安定している 3 秒程度の部分を使用した。
音は、F 管のシングルホルンで、バルブを使用しない
自然倍音列
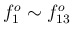 を、
各 10 秒位演奏し、その各音源から出だし付近を除いた
安定している 3 秒程度の部分を使用した。
を、
各 10 秒位演奏し、その各音源から出だし付近を除いた
安定している 3 秒程度の部分を使用した。
なお、ホルンでの録音には YAMAHA サイレントブラスのピックアップミュートを 使用したので、実際にはそのミュートの影響によって ミュートのない状態とは若干音高が違っている可能性はある。 また、演奏者の技量は高くはなく、中高の部活の学生レベルである。
そしてその音源 (WAV フォーマット、2 チャンネル、サンプリング
周波数 44100Hz) の安定部分を FFT (高速離散フーリエ変換) にかけて
周波数解析した。
FFT は
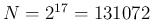 分割をしているので、
周波数分解能は 44100/131072 = 0.34Hz 程度である。
分割をしているので、
周波数分解能は 44100/131072 = 0.34Hz 程度である。
例えば、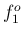 に対するホルンの実音を FFT にかけた結果の
周波数グラフは図 1 のようになる。
なお、すべてのグラフ、およびこれに使用した音声データは、
Web ページ [2] の方にあげる予定である。
に対するホルンの実音を FFT にかけた結果の
周波数グラフは図 1 のようになる。
なお、すべてのグラフ、およびこれに使用した音声データは、
Web ページ [2] の方にあげる予定である。
少しグラフの見方について説明する。 横軸は各音の周波数で、7 次倍音まで含まれる程度の範囲に取っている。
縦軸は、FFT の結果のパワースペクトル 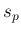 であるが、
その最大値を 1 としたグラフにしている。
なお、
であるが、
その最大値を 1 としたグラフにしている。
なお、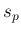 は、通常は FFT の結果の複素数値
は、通常は FFT の結果の複素数値 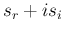 に対して、
その大きさ
に対して、
その大きさ
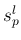 と
と 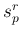 の平均
の平均 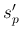 、
あるいは FFT 前にステレオデータの平均を取ってモノラル化したデータを
使って計算した
、
あるいは FFT 前にステレオデータの平均を取ってモノラル化したデータを
使って計算した 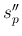 を使っても良かったかもしれないが、
と
を使っても良かったかもしれないが、
と 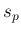 には、
には、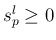 ,
, 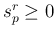 より容易にわかるように
より容易にわかるように
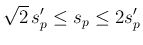
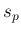 と
と 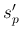 はどちらを使っても大きな違いはない。
一方、
はどちらを使っても大きな違いはない。
一方、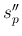 は
なので、
は
なので、
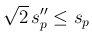
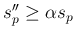 の形の不等式は成り立たない。
それは例えば左右のデータが丁度逆位相だった場合は
の形の不等式は成り立たない。
それは例えば左右のデータが丁度逆位相だった場合は 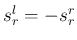 ,
, 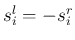 となるので
となるので 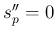 となるが、
となるが、
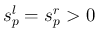 なので
なので 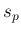 は
は
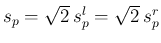 と
なる。今回の目的で言えば、逆位相は起きないだろうが、逆位相のデータが
キャンセルされて 0 になってしまう
と
なる。今回の目的で言えば、逆位相は起きないだろうが、逆位相のデータが
キャンセルされて 0 になってしまう 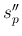 よりも、
むしろ左右のスペクトルをちゃんと拾う
よりも、
むしろ左右のスペクトルをちゃんと拾う 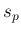 の方が適しているだろうと思う。
の方が適しているだろうと思う。
また、グラフの鉛直な点線は、表 1 で示した
理論的な周波数 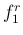 の位置を示す。
の位置を示す。
楽器の実音には、完全な正弦波の純音とは違い多くの倍音成分が含まれる。
すなわち、一つの実音は、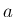 Hz の 1 次成分と
Hz の 1 次成分と 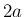 Hz の 2 次の倍音成分 (1 次成分の 1 オクターブ上の音)、
Hz の 2 次の倍音成分 (1 次成分の 1 オクターブ上の音)、
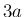 Hz の 3 次の倍音成分 (1 次成分の 1 オクターブ半上の音)、
などの和で構成される。
図 1 のグラフは、
一つの音に含まれる各次数成分の割合を
グラフの高さで表現したものと見ればよい。
ただし、一番高いところが 1 となるようにスケール変換している。
Hz の 3 次の倍音成分 (1 次成分の 1 オクターブ半上の音)、
などの和で構成される。
図 1 のグラフは、
一つの音に含まれる各次数成分の割合を
グラフの高さで表現したものと見ればよい。
ただし、一番高いところが 1 となるようにスケール変換している。
例えば、図 1 の 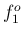 に対するホルンの実音は、
1 次成分の周波数 (
に対するホルンの実音は、
1 次成分の周波数 (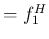 と書く) がほぼ
と書く) がほぼ 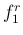 に等しく、
そしてその高さが 1 ということはこの 1 次成分が最大であり、
そしてそれ以外の倍音成分、すなわち
に等しく、
そしてその高さが 1 ということはこの 1 次成分が最大であり、
そしてそれ以外の倍音成分、すなわち 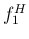 の自然数倍の周波数の音も
かなり強いレベルで、しかもかなり高次成分まで含まれていることがわかる。
の自然数倍の周波数の音も
かなり強いレベルで、しかもかなり高次成分まで含まれていることがわかる。
実際、同じグラフをもっと先の高次成分まで表示したものが 図 2 のグラフであるが、
これによれば、8 倍成分くらいまでかなり大きく、また 14,15 倍成分も 大きくなっていて、かなり高い周波数成分まで含まれていることがわかる。 逆に言えば、より大きな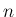 に対する
に対する 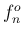 の実音に比べると
あまり純粋な音ではない、と言えるかもしれない。
の実音に比べると
あまり純粋な音ではない、と言えるかもしれない。
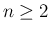 以降のグラフは、
以降のグラフは、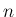 が大きくなるにつれ形はより単純になり、
ほぼ 1 次成分
が大きくなるにつれ形はより単純になり、
ほぼ 1 次成分 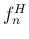 が一番強く、
2 次以降の倍音成分は 1 次成分に比べかなり小さくなっていき、
5 次成分以降はほとんど含まれなくなる。
ただし、
が一番強く、
2 次以降の倍音成分は 1 次成分に比べかなり小さくなっていき、
5 次成分以降はほとんど含まれなくなる。
ただし、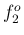 ,
, 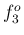 ,
, 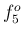 の実音では、
例外的に 1 次成分より 2 次成分の方が強かった。
よって大きい
の実音では、
例外的に 1 次成分より 2 次成分の方が強かった。
よって大きい 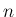 に対する高い自然倍音の実音の方が
純粋な音に近いようにも見える。
に対する高い自然倍音の実音の方が
純粋な音に近いようにも見える。
また、実際のホルンの音 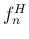 と理論値
と理論値 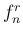 とは、
とは、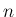 が
大きくなると少しずれが見えてくる。
それにはいくつかの原因が考えられるが、
例えば、演奏者の技量もその要因の一つだろう。
が
大きくなると少しずれが見えてくる。
それにはいくつかの原因が考えられるが、
例えば、演奏者の技量もその要因の一つだろう。
また、実際のホルンの自然倍音は完全に開管の (2) の
形になるわけではなく、あくまでそれに近い形になるだけで ([1])、
特に高次の自然倍音ではそこからのずれが大きくなることが
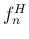 と
と 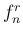 とのずれの原因となりうる。
とのずれの原因となりうる。
他にも、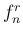 は基準音の A を 440Hz として計算したのであるが、
金管楽器は 440Hz よりも少し高い音を基準として設計されている
可能性があり、それも原因の一つかもしれない。
温度などの環境変化によって、主に音速
は基準音の A を 440Hz として計算したのであるが、
金管楽器は 440Hz よりも少し高い音を基準として設計されている
可能性があり、それも原因の一つかもしれない。
温度などの環境変化によって、主に音速 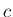 が変わることによって
管楽器の音高は少し変わるが、その調整のために
金管楽器には「チューニング管」というものがついていて、
それを少し抜くことで管全体の長さを長くして全体の音高を少し下げる
ことができる。
しかし、これは長くして下げることができるだけで、
短くすることはできず、上げる方向には調整できないので、
元々楽器の基準が少し高めに設定されている、という可能性が考えられるが、
詳しくはわからない。この基準の高めの設定の可能性については、
6 節でまた考える。
が変わることによって
管楽器の音高は少し変わるが、その調整のために
金管楽器には「チューニング管」というものがついていて、
それを少し抜くことで管全体の長さを長くして全体の音高を少し下げる
ことができる。
しかし、これは長くして下げることができるだけで、
短くすることはできず、上げる方向には調整できないので、
元々楽器の基準が少し高めに設定されている、という可能性が考えられるが、
詳しくはわからない。この基準の高めの設定の可能性については、
6 節でまた考える。
今回の実験で得られた、実際のホルンの 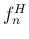 の値、
すなわち自然倍音の 1 次成分周波数を表 2 に示す。
なお、表 2 の 3 列目は、表 1 の
右端に示した
の値、
すなわち自然倍音の 1 次成分周波数を表 2 に示す。
なお、表 2 の 3 列目は、表 1 の
右端に示した 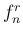 の値、すなわち A=440Hz から計算した F 管ホルンの
自然倍音の理論的な開管周波数、
音高差は
の値、すなわち A=440Hz から計算した F 管ホルンの
自然倍音の理論的な開管周波数、
音高差は 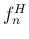 と
と 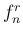 のセント単位での音高差、
すなわち音階数の差の 100 倍
のセント単位での音高差、
すなわち音階数の差の 100 倍
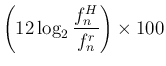
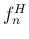 が
が 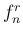 より低い音もあるが、全般的にはやや高めである。
これについても、6 節で考察する。
また、これが開管の式 (2) とどれくらい合っているかに
ついては、5 節で他の実験結果と合わせて考察する。
より低い音もあるが、全般的にはやや高めである。
これについても、6 節で考察する。
また、これが開管の式 (2) とどれくらい合っているかに
ついては、5 節で他の実験結果と合わせて考察する。
竹野茂治@新潟工科大学