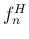
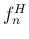 が
が 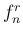 より全般的に高め
であることについて考察してみる。
より全般的に高め
であることについて考察してみる。
とりあえず表 4 の 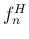 に対する回帰直線を用いて、
この回帰直線での A (440Hz) の音を計算してみると、
それは
に対する回帰直線を用いて、
この回帰直線での A (440Hz) の音を計算してみると、
それは
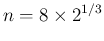 での周波数に対応するので、
での周波数に対応するので、
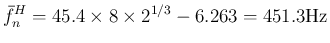
もし A = 450Hz として 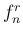 を計算し直すと、
を計算し直すと、
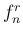 は 450/440 倍され、
音高差は
は 450/440 倍され、
音高差は
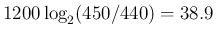 が引き算されるので、
表 2 は表 5 のようになる。
が引き算されるので、
表 2 は表 5 のようになる。
前の 440Hz の方の計算の表 2 では、
30 セント以内のずれの音は 5 つだったが、
こちらは 7 つなのでこちらの方がわずかに 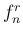 に近い。
ただし、それでもなお 50 セント以上ずれている音が 2 つもあり、
しかもその一方がかなり標準的な音である真ん中のソの音 (
に近い。
ただし、それでもなお 50 セント以上ずれている音が 2 つもあり、
しかもその一方がかなり標準的な音である真ん中のソの音 (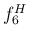 ) で
あることはかなり問題な気がする。
) で
あることはかなり問題な気がする。
もう一方の 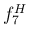 は通常は使わないが、
74 セントも下がるため表 1 の
は通常は使わないが、
74 セントも下がるため表 1 の 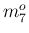 から計算しても
から計算しても
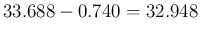 となるので、A
となるので、A 2 (ラ♯) ではなく A2 (ラ) に
なってしまう。
これは実際にそのようで、通常の奏法のラ、
すなわち 1 + 2 番バルブで
2 (ラ♯) ではなく A2 (ラ) に
なってしまう。
これは実際にそのようで、通常の奏法のラ、
すなわち 1 + 2 番バルブで 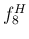 から 3 半音下げた音と、
から 3 半音下げた音と、
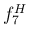 はほぼ同じ音、少なくとも音名としてはどちらもラに聞こえる。
はほぼ同じ音、少なくとも音名としてはどちらもラに聞こえる。
また、上のドである 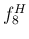 も 30 セントもずれているが、
も 30 セントもずれているが、
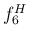 ,
, 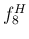 はかなり重要な音なので、
これらが大きくずれているということは、
演奏者の技量に問題があるのかもしれない。
金管楽器の場合、出る音が完全に一定なわけではなく、
同じ音でもマウスピースから送る音の調整によって出る音の高さには
多少ゆらぎ、幅のようなものがある。
次に、その一つの音に対する幅のようなものを測定してみた。
上でかなりずれていた
はかなり重要な音なので、
これらが大きくずれているということは、
演奏者の技量に問題があるのかもしれない。
金管楽器の場合、出る音が完全に一定なわけではなく、
同じ音でもマウスピースから送る音の調整によって出る音の高さには
多少ゆらぎ、幅のようなものがある。
次に、その一つの音に対する幅のようなものを測定してみた。
上でかなりずれていた 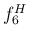 (ソの音) に対して、
高めのソの音と低めのソの音を同じホルンで演奏し、
録音したデータの周波数を調べてみた。
(ソの音) に対して、
高めのソの音と低めのソの音を同じホルンで演奏し、
録音したデータの周波数を調べてみた。
一度フラットに中程度に演奏したものと、低めと高めに演奏したものを
それぞれ 2,3 録音し、1 次成分を拾ってみたところ、
A=450Hz での 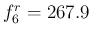 Hz との差は表 6 のようになった (音高差はセント単位)。
Hz との差は表 6 のようになった (音高差はセント単位)。
結局、高め、低めの音は出るといっても、
その最大の幅は 35 セント程度であり、
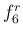 を越える高さのものは安定して出せることはなく、
それより高い音を出そうとすると、次の倍音
を越える高さのものは安定して出せることはなく、
それより高い音を出そうとすると、次の倍音 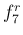 に
はずれてしまっていた。
に
はずれてしまっていた。
つまり、この 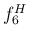 が、
が、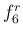 に比べてかなり低いのは、
演奏者の技量というよりも、少なくとも今回に使用した楽器に起こる
現象のように思える。ただし、これが今回使用した楽器固有の癖なのか、
それとも F 管ホルン全般に共通して起こることなのかはわからない。
ただし、F 管ホルンといっても、管が太くなっていく形は、
例えば YAMAHA のホルンだけでも何種類かあり (細ベル、太ベル等)、
そのそれぞれで自然倍音の周波数は変わるだろうから、
どのホルンでも今回の実験と同じようになるとは言えないように思う。
に比べてかなり低いのは、
演奏者の技量というよりも、少なくとも今回に使用した楽器に起こる
現象のように思える。ただし、これが今回使用した楽器固有の癖なのか、
それとも F 管ホルン全般に共通して起こることなのかはわからない。
ただし、F 管ホルンといっても、管が太くなっていく形は、
例えば YAMAHA のホルンだけでも何種類かあり (細ベル、太ベル等)、
そのそれぞれで自然倍音の周波数は変わるだろうから、
どのホルンでも今回の実験と同じようになるとは言えないように思う。
竹野茂治@新潟工科大学