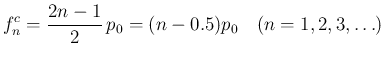 (1)
(1)
高校の物理の気柱の話で学ぶように、 片側が閉じている「閉管」では気柱の共鳴周波数は
となるのだが、これは管の断面積が一定である直管の場合であり、 金管楽器は直管ではなく、出口に向かって内径が徐々に広がり、 出口付近では急激に広がる形をしているため、 共鳴周波数はいわゆる「開管」の場合の にほぼ近い形になることが知られている ([1], [3])。 この周波数を持つ音の列を「自然倍音」と呼ぶ。唇で生成する原音を変化させることで、 ひとつの管長に対して自然倍音列の複数の高さの音を作ることができ、 さらにバルブの操作を加えることで、 自然倍音から少しずつ下がった音を生成できるため、 金管楽器は数オクターブに渡る音階のすべての半音を 出すことができるようになっている。
なお、バルブのない時代のトランペット (バロックトランペット) や
ホルン (ナチュラルホルン) は、
音高が近い高次、すなわち大きい 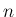 の自然倍音列を利用することで
出せる音の高さの種類を増やしたり、
さらにホルンでは出口に手を入れて出口の長さや広さを手の形で
操作することで半音から 1 音程度の音高を下げる奏法などを使うことで
多くの高さの音を出したりすることが行われていたようである ([4])。
の自然倍音列を利用することで
出せる音の高さの種類を増やしたり、
さらにホルンでは出口に手を入れて出口の長さや広さを手の形で
操作することで半音から 1 音程度の音高を下げる奏法などを使うことで
多くの高さの音を出したりすることが行われていたようである ([4])。
以下に自然倍音の音高を示すが、
周波数が 2 倍になると音高は丁度 1 オクターブ上がり、
1 オクターブには半音が 12 音入っているので、
1 半音上げることは周波数を
![$2^{1/12}=\sqrt[12]{2}$](img14.png) 倍することに
対応する (平均律音階の場合)。
すなわち、自然倍音 (2) の周波数
倍することに
対応する (平均律音階の場合)。
すなわち、自然倍音 (2) の周波数 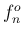 に対して、
「音階数」
に対して、
「音階数」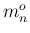 を
を
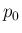 との音の高さの差、
すなわち
との音の高さの差、
すなわち 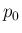 を基音とする半音階の音程を表現することになる。
その数値が整数に近ければその半音階に良く沿った音であるが、
整数から遠い場合はその半音階からは少し外れた音であることになる。
なお、本稿の「音階数」という呼び名は一般的なものではない。
を基音とする半音階の音程を表現することになる。
その数値が整数に近ければその半音階に良く沿った音であるが、
整数から遠い場合はその半音階からは少し外れた音であることになる。
なお、本稿の「音階数」という呼び名は一般的なものではない。
表 1 に、自然倍音列の音高を示す。 なお、音名の表記は、1 オクターブ (ドからその上のシまで) の 12 音に C から G, および A, B で
C = ド、Cとしていて、その後ろにオクターブ番号、すなわち 1 大きいと 1 オクターブ上の高さの音を意味する数字を追加した形で表している。= ド♯、 D = レ、D
= レ♯、 E = ミ、 F = ファ、
F= ファ♯、 G = ソ、G
= ソ♯、 A = ラ、A
= ラ♯、 B = シ
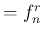 と書く) とは、
F 管のシングルホルンの場合のバルブを使わない管長での
と書く) とは、
F 管のシングルホルンの場合のバルブを使わない管長での 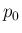 から
計算した周波数 (理論上の値) である。
これは以下のように計算している。
から
計算した周波数 (理論上の値) である。
これは以下のように計算している。
F 管シングルホルンでは、通常のホルンの楽譜の「下のド」(F 管なので C 調のピアノで言えば F の音) は 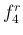 で、「上のド」は
で、「上のド」は 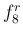 になる。
よく基準音として使われる 440Hz の C 調での A (ラ) は、
ホルンで言えば
になる。
よく基準音として使われる 440Hz の C 調での A (ラ) は、
ホルンで言えば 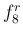 の F の 2 音 (4 半音) 上の音になるので、
の F の 2 音 (4 半音) 上の音になるので、
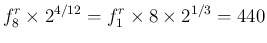
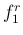 は
となる。あとは開管の式 (2) に従って
その整数倍
は
となる。あとは開管の式 (2) に従って
その整数倍
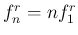 により計算したものである。
により計算したものである。
さて、表 1 を見ると、例えば以下のようないくつかのことが わかる。
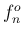 と
と 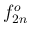 は 1 オクターブ違う音高になる
(
は 1 オクターブ違う音高になる
(
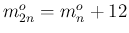 )。
)。
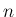 では音階としての (周波数ではなく音階数としての) 音高の間隔が広く、大きい
では音階としての (周波数ではなく音階数としての) 音高の間隔が広く、大きい 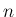 では音高の間隔が狭い。
では音高の間隔が狭い。
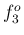 ,
, 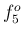 ,
, 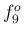 などは整数とのずれがそれほど大きくはないので、
ある程度音階に沿った音高だが、
などは整数とのずれがそれほど大きくはないので、
ある程度音階に沿った音高だが、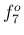 ,
, 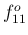 ,
, 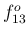 などは
整数とのずれが大きく、音階からかなり外れた音になる。
などは
整数とのずれが大きく、音階からかなり外れた音になる。
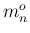 が
が 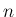 の対数なので、
の対数なので、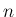 の増加に
伴って
の増加に
伴って 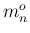 の増加速度が遅くなることによる。
そしてそのことにより、以下の性質が生まれる。
の増加速度が遅くなることによる。
そしてそのことにより、以下の性質が生まれる。
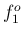 と
と 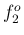 の間では 3 つのバルブだけでは不可能。
の間では 3 つのバルブだけでは不可能。
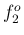 と
と 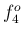 の間なら、3 つのバルブでもすべての半音を実現可能
(
の間なら、3 つのバルブでもすべての半音を実現可能
(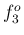 から 6 半音下げれば C
から 6 半音下げれば C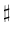 1 が出せ、
1 が出せ、
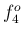 から 4 半音下げれば G
から 4 半音下げれば G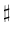 1 が出せる)。
1 が出せる)。
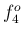 と
と 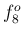 の間は、
の間は、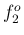 と
と 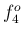 の間よりも
自然倍音が多いので、その分バルブ操作も少なくできる。
の間よりも
自然倍音が多いので、その分バルブ操作も少なくできる。
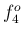 と
と 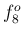 の方が
の方が 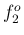 と
と 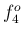 の間よりも
自然倍音同士が近いので、唇で適切な自然倍音を選別するのが難しくなる
の間よりも
自然倍音同士が近いので、唇で適切な自然倍音を選別するのが難しくなる
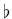 管) では
「下のド」と「上のド」は
管) では
「下のド」と「上のド」は 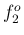 と
と 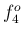 に対応し、
F 管のシングルホルンでは
に対応し、
F 管のシングルホルンでは 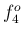 と
と 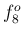 に対応しているため、
トランペットの方が指使いは多少複雑だが、音程は安定しやすく、
ホルンの方が指使いはシンプルだが、音程が安定せず、
狙った音を外しやすい性質がある。
そのためホルンはオーケストラ内で最も難しい楽器の一つと
呼ばれることもある。
に対応しているため、
トランペットの方が指使いは多少複雑だが、音程は安定しやすく、
ホルンの方が指使いはシンプルだが、音程が安定せず、
狙った音を外しやすい性質がある。
そのためホルンはオーケストラ内で最も難しい楽器の一つと
呼ばれることもある。
竹野茂治@新潟工科大学