5 複素数を利用した三角関数の有理関数の積分
三角関数は、複素数を用いて指数関数に直す方が、
式の操作が容易になる場合が多い。
例えば、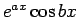 のような関数の積分は、
通常は 2 回の部分積分により元の積分の定数倍の式を導いて、
のような関数の積分は、
通常は 2 回の部分積分により元の積分の定数倍の式を導いて、
とし、右辺の 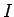 の項を左辺に移行して、
の項を左辺に移行して、
より
という形で求めるが、これを複素数を用いて、
とする方が部分積分による方法よりも直感的、機械的で分かりやすい。
これと同様のことを 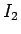 に対して考えてみる。
に対して考えてみる。
オイラーの公式
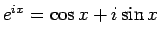 より、
より、
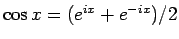 と書けるから、
と書けるから、
となる。形式的には、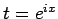 と置くと
と置くと 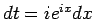 なので、
なので、
となるが、このようにすると 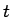 は実数変数ではなく、複素数変数となり、
厳密には複素関数論の線積分になってしまい、
実数変数の複素数値関数の範囲を越えてしまう。
よって、ここではそれを避け、(9) を
利用することにする。
すなわち、分子の
は実数変数ではなく、複素数変数となり、
厳密には複素関数論の線積分になってしまい、
実数変数の複素数値関数の範囲を越えてしまう。
よって、ここではそれを避け、(9) を
利用することにする。
すなわち、分子の 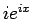 は使わずに、
は使わずに、
の形の部分分数分解を行い、それにより 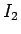 を
を
のように変形して (9) を適用して
複素対数で表す、という方針である。
まず、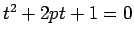 の解は、
の解は、
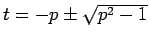 (
(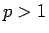 より
実数解) なので、
より
実数解) なので、
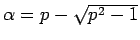 ,
,
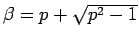 とすれば、
とすれば、
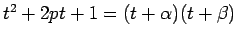 と因数分解される。
なお、解と係数の関係より
と因数分解される。
なお、解と係数の関係より 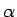 は
は
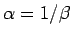 と
書けることに注意する。
これにより、
と
書けることに注意する。
これにより、
となるので、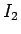 は
は
と書ける。
ここで、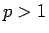 より
より
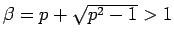 であり、
であり、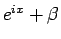 は、
は、
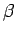 中心の半径 1 の円周上を動くので、実軸の左半分とは
交わらない (図 5 の右側の円)。
一方、
中心の半径 1 の円周上を動くので、実軸の左半分とは
交わらない (図 5 の右側の円)。
一方、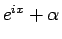 も
も 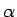 中心の半径 1 の円周上を動くが、
中心の半径 1 の円周上を動くが、
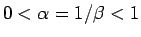 だからその円周の内部に原点があり、
実軸の左半分とこの円周とは交わる (図 5 の左側の円)。
だからその円周の内部に原点があり、
実軸の左半分とこの円周とは交わる (図 5 の左側の円)。
図 5:
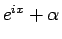 と
と 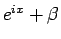 の描く円
の描く円
|
|
よって、とりあえず 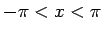 の範囲で考えることにすれば、
の範囲で考えることにすれば、
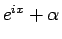 は実軸の左半分とは交わらない。
この範囲では、(9) により
は実軸の左半分とは交わらない。
この範囲では、(9) により
となる。ここで、命題 1 より、
であり、
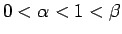 より、
より、
なので、いずれにせよ
となり、よってこれは主値の範囲なので、
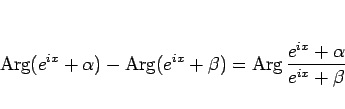 |
(20) |
となることがわかる。
なお、このような 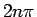 の差や主値の範囲の議論は不定積分では省略し、
の差や主値の範囲の議論は不定積分では省略し、
として、最後の定数の部分は積分定数に含めて済ませてしまうことも多い。
結局 (20) により、(19) は
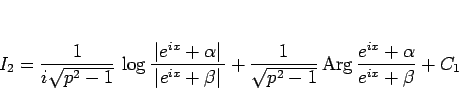 |
(21) |
となる。次は、このそれぞれの項を見てみる。
まず、
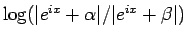 であるが、
であるが、
であり、
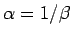 だったので、
だったので、
となる。よって、この対数の項は
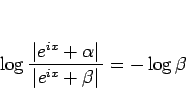 |
(22) |
と定数になり、この部分は積分定数に取り込まれることになる (実際は
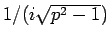 倍がつくので純虚数の定数)。
なお、この計算は、
倍がつくので純虚数の定数)。
なお、この計算は、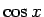 ,
, 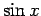 に直さなくても、
最初から
に直さなくても、
最初から
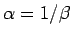 を使って、
を使って、
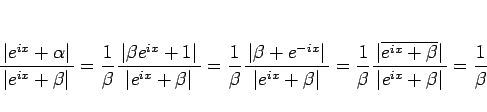 |
(23) |
とすることもできる (少し高度) し、元々  は実数値なので、
(21) の実数部分のみ考えればよく、
よって
は実数値なので、
(21) の実数部分のみ考えればよく、
よって  の方の項は最初から不要である、と見ることもできる。
の方の項は最初から不要である、と見ることもできる。
次は、
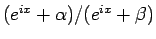 の偏角であるが、
正の実数
の偏角であるが、
正の実数 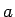 に対して
に対して
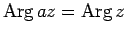 となること、
および
となること、
および
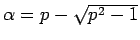 ,
,
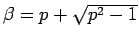 ,
,
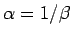 であることに注意すると、
であることに注意すると、
となるが、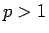 より
より 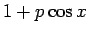 は、
は、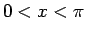 の範囲、
および
の範囲、
および 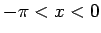 の範囲で符号が変わりうるので、
(6) ではなく (7) を
用いると
の範囲で符号が変わりうるので、
(6) ではなく (7) を
用いると
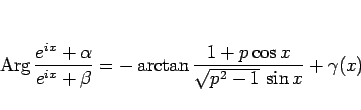 |
(24) |
と書くことができる。ここで 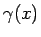 は、
は、
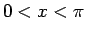 ならば
ならば
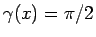 ,
,
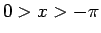 ならば
ならば
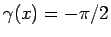 である。
なお、(24) の右辺は一見
である。
なお、(24) の右辺は一見 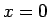 で不連続なようだが、
で不連続なようだが、
となり、連続になっている。
(21), (22), (24) より 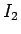 は、
は、
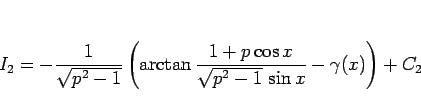 |
(25) |
となる。しかし、この式と (14) とは
かなり違った形になっている。
偏角の計算で他の方法を取ると、また違う式が得られる。
 を用いると、
を用いると、
と書けるが、
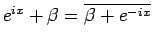 より
より
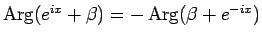 なので、
なので、
となる。
なお、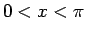 のとき
のとき
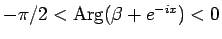 より
より
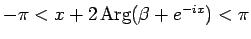 で、
で、
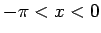 のときも
のときも
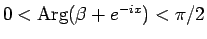 より
より
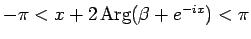 となるから、
この式には
となるから、
この式には 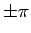 は必要ない。
は必要ない。
よって、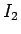 は
は
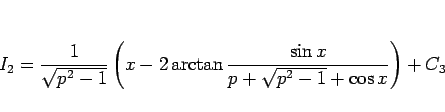 |
(26) |
とも書けることになる。
さらに、最初から (14) を意識し、分子分母を 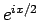 で
割って
で
割って
と変形すると、この分母は分子の共役なので、
となる。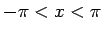 より
より 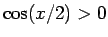 なので、
(6) より、
なので、
(6) より、
となるが、
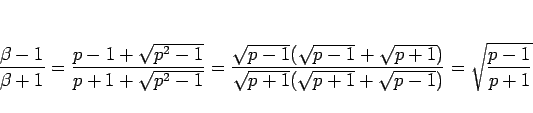 |
(27) |
なので、結局
となり、よって、(21), (22) よりこの場合は直接 (14) が得られることがわかる。
さて、(25), (26) と (14) の
関係についても見ておこう。
まず、(25) であるが、 と書くこととし、
倍角の公式を用いると、
と書くこととし、
倍角の公式を用いると、
となるので、
と書ける。ここで、
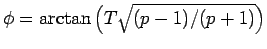 と
すると、
と
すると、
となる。
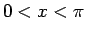 なら
なら 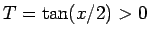 より
より 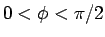 、よって
、よって
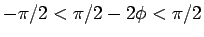 となるので、
となるので、
となる。
同様に、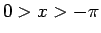 なら
なら 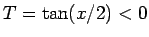 より
より 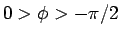 、
よって
、
よって
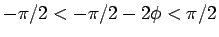 となるので、
となるので、
となる。よって、いずれの場合も、
となるので、よって 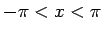 の範囲で (25) は
確かに (14) に一致することがわかる。
の範囲で (25) は
確かに (14) に一致することがわかる。
次は (26) と (14) の関係を見る。
となるが、次の加法定理によりこれを一つにまとめることができる。
命題 4
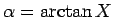 ,
,
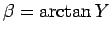 に対して、
に対して、
-
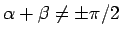 のとき、
のとき、
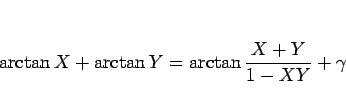 |
(29) |
ここで 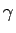 は、
は、
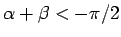 ならば
ならば 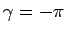 ,
,
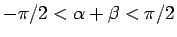 ならば
ならば 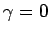 ,
,
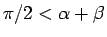 ならば
ならば 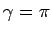 。
。
-
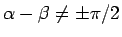 のとき、
のとき、
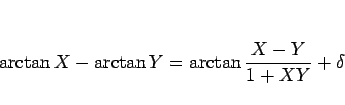 |
(30) |
ここで 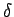 は、
は、
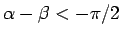 ならば
ならば 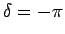 ,
,
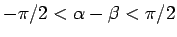 ならば
ならば 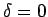 ,
,
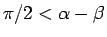 ならば
ならば 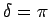 。
。
証明
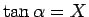 ,
, 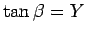 より、
より、
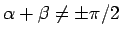 のとき、
のとき、
となる。よって、
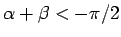 ならば、
ならば、
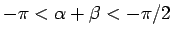 より
より
なので、
となり、よって
が得られる。
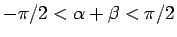 の場合、
の場合、
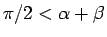 の場合も同様である。
の場合も同様である。
(30) は、(29) で 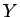 を
を 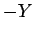 と
すれば得られる。
と
すれば得られる。
今、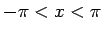 として (28) の
として (28) の 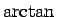 の差を
考えると、
の差を
考えると、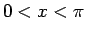 ならば
ならば 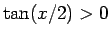 ,
,
 より
それらの
より
それらの 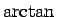 の値はそれぞれ
の値はそれぞれ 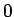 から
から 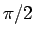 の間にあり、
その差は
の間にあり、
その差は 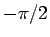 から
から 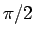 の間にある。
の間にある。
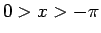 の場合も
の場合も 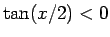 ,
,
 より
それらの
より
それらの 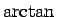 の差は
の差は 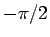 から
から 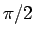 の間にある。
よって、命題 4 により
の間にある。
よって、命題 4 により
となる。
ここで、前と同様に  とすれば、
とすれば、
より、
(27) より、
となることがわかる。
これと (28) により、
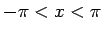 では (26) が (14) に
一致することがわかる。
では (26) が (14) に
一致することがわかる。
しかも、(26) の右辺のかっこの中の式を 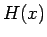 と
すると、
と
すると、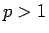 より
より 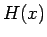 はすべての
はすべての 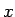 に対して滑らかであり、
明らかに
に対して滑らかであり、
明らかに 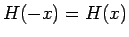 ,
,
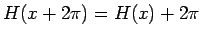 が成り立つので、
この
が成り立つので、
この 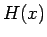 は実は (18) の
は実は (18) の
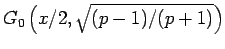 に等しく、
つまり (26) は、
に等しく、
つまり (26) は、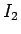 の、すべての
の、すべての 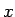 で連続な
原始関数を与えていることがわかる。
で連続な
原始関数を与えていることがわかる。
(14) の式は元々 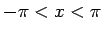 に対してしか成り立たず、
すべての
に対してしか成り立たず、
すべての 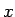 に対して滑らかな原始関数を持つはずの
に対して滑らかな原始関数を持つはずの 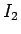 を
表現するためには、(18) のように
を
表現するためには、(18) のように 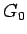 を
導入しなければいけなかったが、
それは実は (26) のような式で容易に表わされることがわかり、
よって (14) よりも (26) の方が
むしろ優れていると見ることもできる。
を
導入しなければいけなかったが、
それは実は (26) のような式で容易に表わされることがわかり、
よって (14) よりも (26) の方が
むしろ優れていると見ることもできる。
しかし、逆に複素数を使わずに普通に置換積分による不定積分を行っても、
なかなか (26) の式にはたどりつけない。
竹野茂治@新潟工科大学
2016年12月22日
![]() より、
より、
![]() と書けるから、
と書けるから、
![]() の解は、
の解は、
![]() (
(![]() より
実数解) なので、
より
実数解) なので、
![]() ,
,
![]() とすれば、
とすれば、
![]() と因数分解される。
なお、解と係数の関係より
と因数分解される。
なお、解と係数の関係より ![]() は
は
![]() と
書けることに注意する。
これにより、
と
書けることに注意する。
これにより、
![]() より
より
![]() であり、
であり、![]() は、
は、
![]() 中心の半径 1 の円周上を動くので、実軸の左半分とは
交わらない (図 5 の右側の円)。
一方、
中心の半径 1 の円周上を動くので、実軸の左半分とは
交わらない (図 5 の右側の円)。
一方、![]() も
も ![]() 中心の半径 1 の円周上を動くが、
中心の半径 1 の円周上を動くが、
![]() だからその円周の内部に原点があり、
実軸の左半分とこの円周とは交わる (図 5 の左側の円)。
だからその円周の内部に原点があり、
実軸の左半分とこの円周とは交わる (図 5 の左側の円)。
![]() であるが、
であるが、
![]() の偏角であるが、
正の実数
の偏角であるが、
正の実数 ![]() に対して
に対して
![]() となること、
および
となること、
および
![]() ,
,
![]() ,
,
![]() であることに注意すると、
であることに注意すると、
![]() を用いると、
を用いると、
![]() のとき
のとき
![]() より
より
![]() で、
で、
![]() のときも
のときも
![]() より
より
![]() となるから、
この式には
となるから、
この式には ![]() は必要ない。
は必要ない。
![]() は
は
![]() で
割って
で
割って
![]() と書くこととし、
倍角の公式を用いると、
と書くこととし、
倍角の公式を用いると、
![]() なら
なら ![]() より
より ![]() 、よって
、よって
![]() となるので、
となるので、
![]() ,
,
![]() に対して、
に対して、
![]() ,
, ![]() より、
より、
![]() のとき、
のとき、
![]() として (28) の
として (28) の ![]() の差を
考えると、
の差を
考えると、![]() ならば
ならば ![]() ,
,
![]() より
それらの
より
それらの ![]() の値はそれぞれ
の値はそれぞれ ![]() から
から ![]() の間にあり、
その差は
の間にあり、
その差は ![]() から
から ![]() の間にある。
の間にある。
![]() の場合も
の場合も ![]() ,
,
![]() より
それらの
より
それらの ![]() の差は
の差は ![]() から
から ![]() の間にある。
よって、命題 4 により
の間にある。
よって、命題 4 により
![]() と
すると、
と
すると、![]() より
より ![]() はすべての
はすべての ![]() に対して滑らかであり、
明らかに
に対して滑らかであり、
明らかに ![]() ,
,
![]() が成り立つので、
この
が成り立つので、
この ![]() は実は (18) の
は実は (18) の
![]() に等しく、
つまり (26) は、
に等しく、
つまり (26) は、![]() の、すべての
の、すべての ![]() で連続な
原始関数を与えていることがわかる。
で連続な
原始関数を与えていることがわかる。
![]() に対してしか成り立たず、
すべての
に対してしか成り立たず、
すべての ![]() に対して滑らかな原始関数を持つはずの
に対して滑らかな原始関数を持つはずの ![]() を
表現するためには、(18) のように
を
表現するためには、(18) のように ![]() を
導入しなければいけなかったが、
それは実は (26) のような式で容易に表わされることがわかり、
よって (14) よりも (26) の方が
むしろ優れていると見ることもできる。
を
導入しなければいけなかったが、
それは実は (26) のような式で容易に表わされることがわかり、
よって (14) よりも (26) の方が
むしろ優れていると見ることもできる。