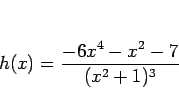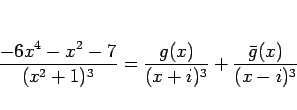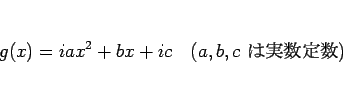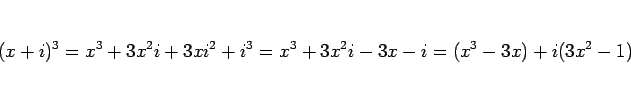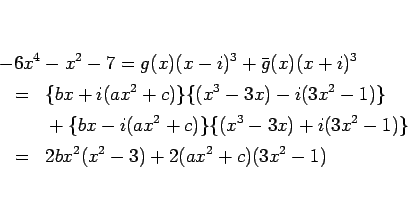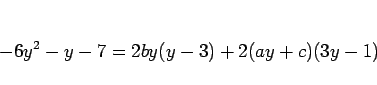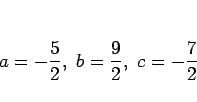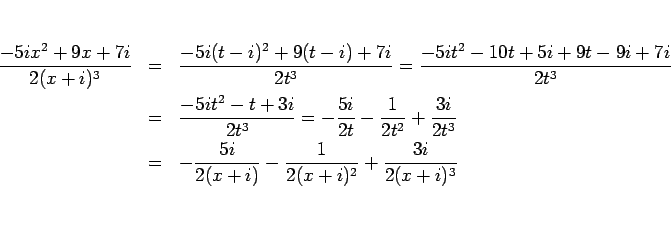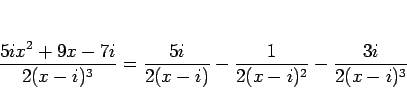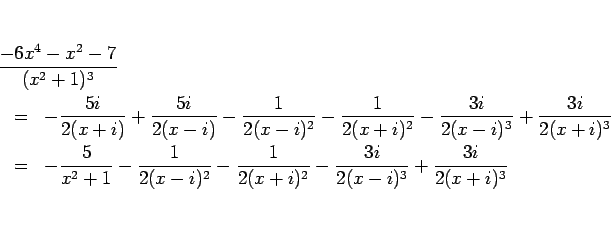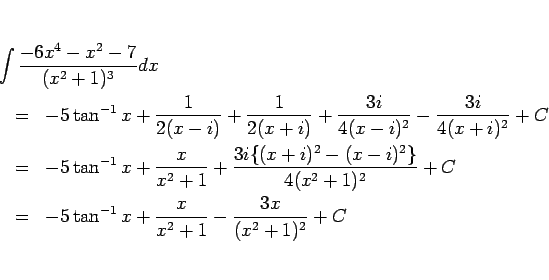次へ: 6 最後に
上へ: 複素数を利用した有理関数の積分
前へ: 4 補題の証明
(PDF ファイル: quotef4.pdf)
5 具体例の計算
ここでは、[2] で計算した例の偶数次の部分
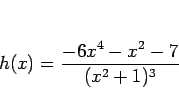 |
(13) |
を利用し、命題 1 を用いて複素数の範囲で分解し、
積分を行うとにする。今の場合、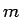 が奇数なので、
が奇数なので、
と分けると、高々 2 次式である 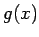 は命題 1 により
は命題 1 により
と書けることになる。
であるから、
となる。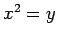 と置けば
と置けば
となる。ここから係数比較、あるいは 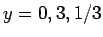 等を代入すれば、
等を代入すれば、
となることがわかる。よって、
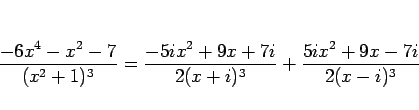 |
(14) |
となる。この右辺の最初の式で 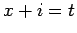 と置くと、
と置くと、
と分けられることがわかる。(14) の右辺の 2 つ目の項は
この式の共役複素数であるから、
となる。
分母が一次式の場合は、積分を考えるのは少し厄介なので
(複素対数関数を考えないといけない)、
それは共役なものと通分してまとめると、
となる。この式を積分すると、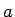 が複素数であっても
が複素数であっても 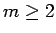 のときは
のときは
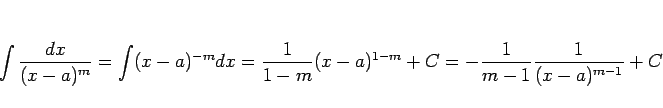 |
(15) |
が成り立つ (証明は A 節参照) ので、
となる。
次へ: 6 最後に
上へ: 複素数を利用した有理関数の積分
前へ: 4 補題の証明
竹野茂治@新潟工科大学
2006年6月2日