(6) の ![]() ,
, ![]() は互いに素。
よって、(6) の
は互いに素。
よって、(6) の ![]() と
と ![]() ,
,
![]() と
と ![]() も互いに素。
も互いに素。
証明
実数係数の整式 ![]() ,
, ![]() が互いに素ではないとすると、
[3] の 命題 8, 系 9 を利用すれば、
その共通因子は実数係数の整式と取れることがわかる。
それを
が互いに素ではないとすると、
[3] の 命題 8, 系 9 を利用すれば、
その共通因子は実数係数の整式と取れることがわかる。
それを ![]() (最高次の係数を 1 とする) とし、
(最高次の係数を 1 とする) とし、
![]() ,
, ![]() を
を ![]() で割った商をそれぞれ
で割った商をそれぞれ
![]() ,
, ![]() とすると、
とすると、![]() ,
, ![]() であるので、
であるので、
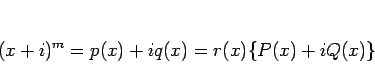
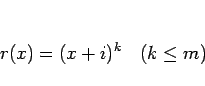
![]() ,
, ![]() が互いに素なので、例えば
が互いに素なので、例えば ![]() が偶数の場合、
が偶数の場合、
![]() ,
,
![]() も互いに素となる
(もし
も互いに素となる
(もし ![]() ,
, ![]() に共通因子があれば、
に共通因子があれば、
![]() ,
, ![]() が共通因子を持つことになる)。
が共通因子を持つことになる)。
![]() が奇数の場合も同様。
が奇数の場合も同様。