次へ: 4 補題の証明
上へ: 複素数を利用した有理関数の積分
前へ: 2 共役による対称性
(PDF ファイル: quotef4.pdf)
3 偶数次、奇数次による対称性
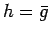 により (2) は、
により (2) は、
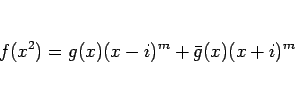 |
(5) |
になるが、左辺が偶数次の項のみなので、
これを利用すると 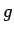 の形はもう少し限定することができる。
の形はもう少し限定することができる。
容易にわかるように、
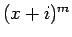 は、
は、
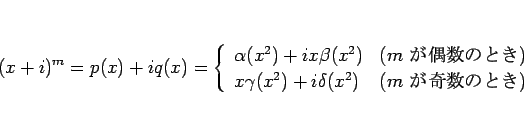 |
(6) |
のように書ける。
ここで、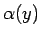 ,
, 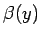 ,
, 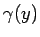 ,
, 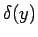 は
実数係数の整式で、その次数は
は
実数係数の整式で、その次数は
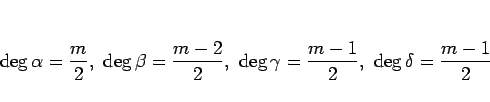 |
(7) |
となる。
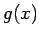 の係数を実数部分と虚数部分に分離して、
の係数を実数部分と虚数部分に分離して、
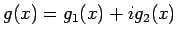 (
(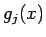 は実数係数の整式) とすると、
は実数係数の整式) とすると、
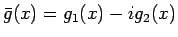 であり、
また
であり、
また
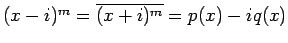 であるから、
(5) より、
であるから、
(5) より、
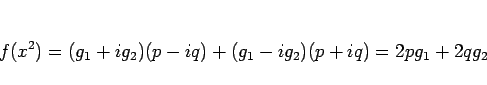 |
(8) |
となる。
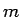 が偶数の場合、
が偶数の場合、
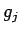 は高々
は高々 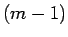 次の多項式だから、それを偶数次と奇数次に分けて
次の多項式だから、それを偶数次と奇数次に分けて
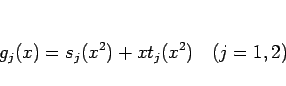 |
(9) |
のようにすると、
であり、(6), (8) より、
となる。左辺は偶数次の項しかないので、右辺の奇数次の項の和は 0、
すなわち
が成り立つことになる。よってすべての 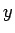 に対し、
に対し、
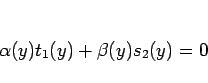 |
(10) |
が成り立つ。
しかし、後で示すように、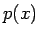 と
と 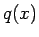 は互いに素なので、
は互いに素なので、
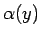 と
と 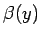 も互いに素であり、この式の多項式の次数は
も互いに素であり、この式の多項式の次数は
となっている。(10) より、
であり、左辺の因子 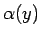 は右辺の因子でもあり、
は右辺の因子でもあり、
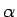 と
と 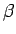 は互いに素なので、
は互いに素なので、
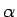 は
は 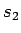 の因子でなければいけないが、
次数を比較すれば
の因子でなければいけないが、
次数を比較すれば 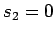 でなければならないことがわかる。
よって、
でなければならないことがわかる。
よって、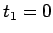 にもなる。
にもなる。
結局、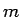 が偶数の場合は、
が偶数の場合は、
となるので 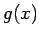 は
は
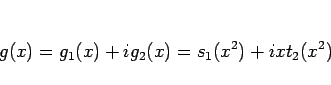 |
(11) |
の形になることになる。
同じように 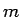 が奇数の場合を考えてみると、
が奇数の場合を考えてみると、
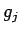 は高々
は高々 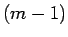 次の多項式だから、
同様に (9) のように分けると、
次の多項式だから、
同様に (9) のように分けると、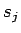 ,
, 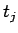 の次数は
の次数は
となる。(6), (8) より、
となり、この場合は
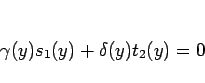 |
(12) |
が成り立つ。
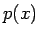 と
と 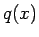 が互いに素なのでこの
が互いに素なのでこの 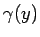 と
と 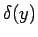 も
互いに素で、次数は
も
互いに素で、次数は
であるから、
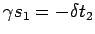 を考えると
を考えると
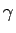 と
と 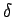 は互いに素なので
は互いに素なので
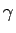 は
は 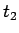 の因子でなければならないが、
次数を比較すればそれは
の因子でなければならないが、
次数を比較すればそれは 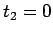 を意味し、よって
を意味し、よって 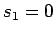 にもなる。
にもなる。
よって、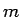 が奇数の場合は、
が奇数の場合は、
となることになる。
以上をまとめると、以下のようになる。
命題 1
(5) を満たす高々 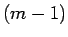 次の整式
次の整式 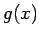 は、
は、
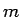 が偶数の場合は、偶数次の係数は実数、奇数次の係数は純虚数
が偶数の場合は、偶数次の係数は実数、奇数次の係数は純虚数
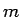 が奇数の場合は、奇数次の係数は実数、偶数次の係数は純虚数
が奇数の場合は、奇数次の係数は実数、偶数次の係数は純虚数
でなければならない。
次へ: 4 補題の証明
上へ: 複素数を利用した有理関数の積分
前へ: 2 共役による対称性
竹野茂治@新潟工科大学
2006年6月2日
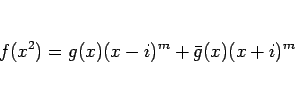
![]() は、
は、
![]() の係数を実数部分と虚数部分に分離して、
の係数を実数部分と虚数部分に分離して、
![]() (
(![]() は実数係数の整式) とすると、
は実数係数の整式) とすると、
![]() であり、
また
であり、
また
![]() であるから、
(5) より、
であるから、
(5) より、
![]() が偶数の場合、
が偶数の場合、
![]() は高々
は高々 ![]() 次の多項式だから、それを偶数次と奇数次に分けて
次の多項式だから、それを偶数次と奇数次に分けて
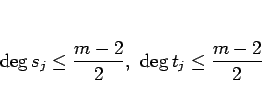
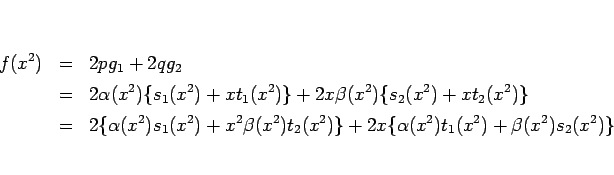
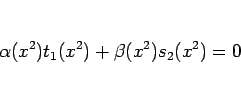
![]() と
と ![]() は互いに素なので、
は互いに素なので、
![]() と
と ![]() も互いに素であり、この式の多項式の次数は
も互いに素であり、この式の多項式の次数は
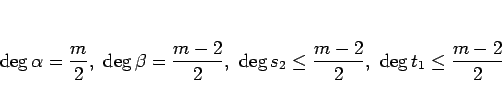
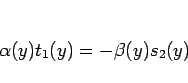
![]() が偶数の場合は、
が偶数の場合は、
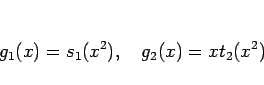
![]() が奇数の場合を考えてみると、
が奇数の場合を考えてみると、
![]() は高々
は高々 ![]() 次の多項式だから、
同様に (9) のように分けると、
次の多項式だから、
同様に (9) のように分けると、![]() ,
, ![]() の次数は
の次数は
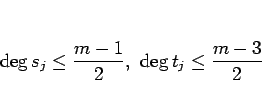
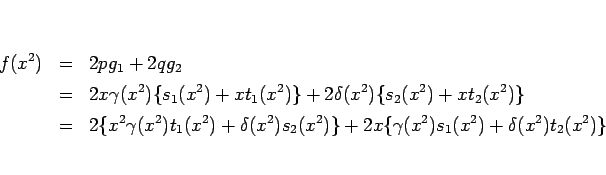
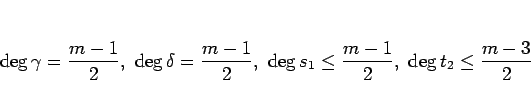
![]() が奇数の場合は、
が奇数の場合は、
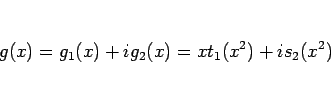
![]() 次の整式
次の整式 ![]() は、
は、