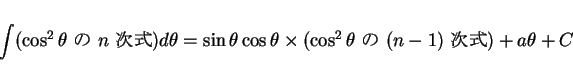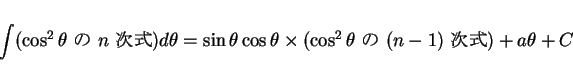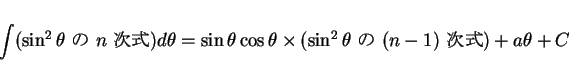

Next: この文書について...
Up: 有理関数の積分について
Previous: 4.3 部分積分で次数を落とす方法
(PDF ファイル: quotef1.pdf)
例を見てもわかると思うが、いずれの方法もかなり計算は煩雑である。
個々の公式よりも、どういう方法でやれば計算できるか、
という計算方法の原理、あるいは全体の計算の流れを正しく把握することが
大事だろうと思われる。
なお、4.1 節で見たことと同様にして
が成り立つ。
そして、個人的な意見であるが、これが成り立つということがわかっていれば、
左辺を計算する場合にこれらの式を導くのと同じ道をたどる、
すなわち部分積分により次数を落としていくという方法を取るよりも、
例 1 のように
未定係数法によって係数のみ決定する方法を取る方が、
微分の計算のみで済むという点で、確実でかつ楽な方法ではないかと思う。


Next: この文書について...
Up: 有理関数の積分について
Previous: 4.3 部分積分で次数を落とす方法
Shigeharu TAKENO
2003年 5月 26日