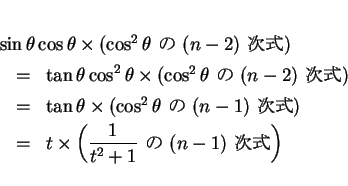

Next: 4.2 4.1
Up: 4 分子が偶数次の項の場合
Previous: 4 分子が偶数次の項の場合
(PDF ファイル: quotef1.pdf)
4.1 t=tanθと置換する方法
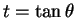 と置換すると、
と置換すると、
より
となり、
となる。
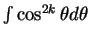 (
(
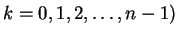 の積分は、
通常は部分積分を使って次数を落としてくやり方で説明することが多いようであるが、
それは以下のようにしても説明できる。
の積分は、
通常は部分積分を使って次数を落としてくやり方で説明することが多いようであるが、
それは以下のようにしても説明できる。
より、
となるので、これを積分して
となる。こうやって 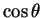 の次数を落としながら整理して行く方法である。
の次数を落としながら整理して行く方法である。
そして結果として、
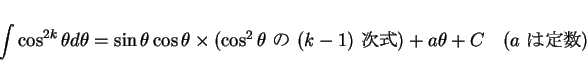 |
(1) |
となるので、結局
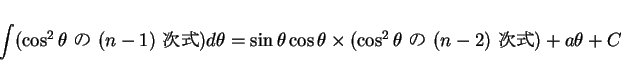 |
(2) |
の形になることになる。
なお、これは上で述べたように次数を落としながら整理せずとも、
この結果を利用して未定係数法で求めるということも可能である。
例 1
積分
を未定係数法で求める。(1) より、
なので、
とする (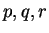 は未定係数)。この式の両辺を微分すると
は未定係数)。この式の両辺を微分すると
となるが、この右辺をさらに 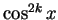 の形の項のみの式に変形する。
の形の項のみの式に変形する。
これが
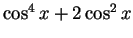 に等しいので、
に等しいので、
となればよい。この連立方程式を解けば 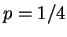 ,
, 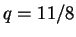 ,
, 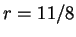 となり、
ゆえに
となり、
ゆえに
となる。
なお、この例で連立一次方程式を導くときに両辺の係数を比較したが、
これは厳密には関数列
が線形独立である、という性質を利用していることになる。
その事実の証明は難しくはないが、やや長くなるのでここでは省略する。
結果として、積分は 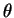 を用いた式としては (2) のように
書けることになるが、これを
を用いた式としては (2) のように
書けることになるが、これを 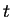 の式に戻すには、
の式に戻すには、
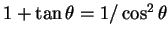 を用いて以下のようにする。
を用いて以下のようにする。
であり、
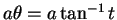 (
(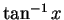 は
は 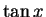 の逆関数) なので、
結局
の逆関数) なので、
結局
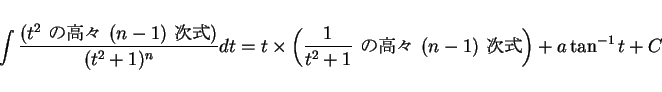 |
(3) |
のようになることになる。


Next: 4.2 4.1
Up: 4 分子が偶数次の項の場合
Previous: 4 分子が偶数次の項の場合
Shigeharu TAKENO
2003年 5月 26日
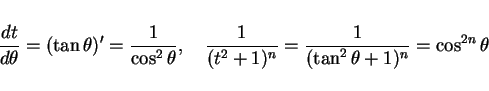
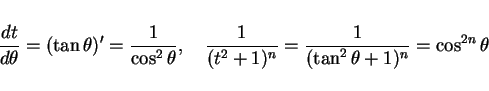
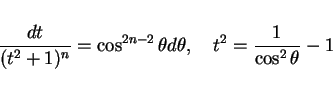
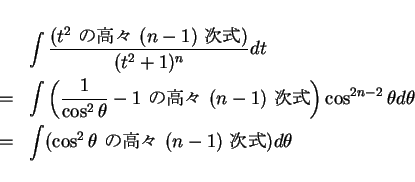
![]() (
(
![]() の積分は、
通常は部分積分を使って次数を落としてくやり方で説明することが多いようであるが、
それは以下のようにしても説明できる。
の積分は、
通常は部分積分を使って次数を落としてくやり方で説明することが多いようであるが、
それは以下のようにしても説明できる。
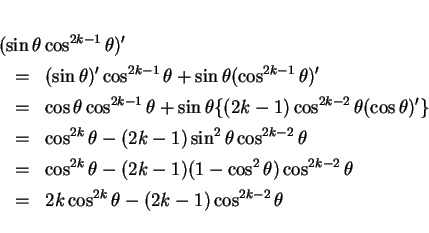
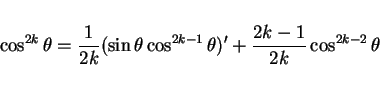
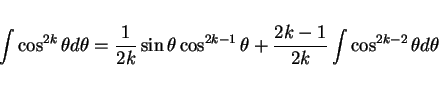
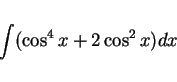
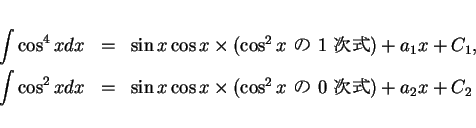
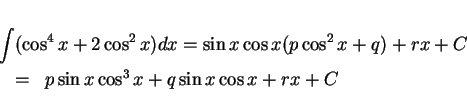
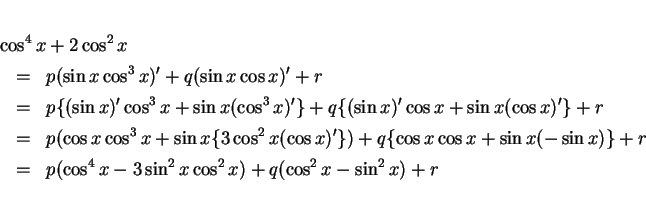
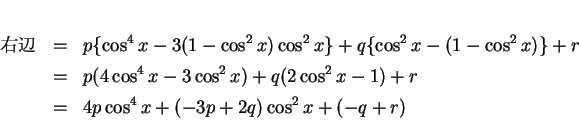
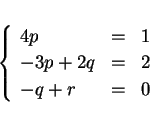
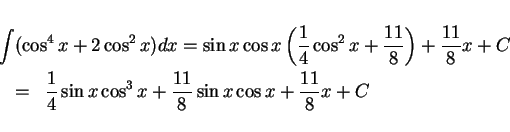
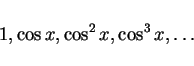
![]() を用いた式としては (2) のように
書けることになるが、これを
を用いた式としては (2) のように
書けることになるが、これを ![]() の式に戻すには、
の式に戻すには、
![]() を用いて以下のようにする。
を用いて以下のようにする。