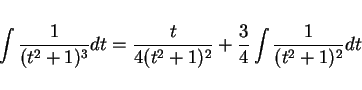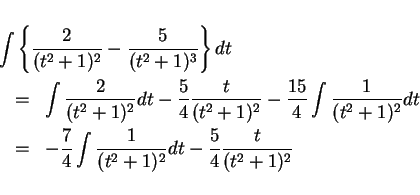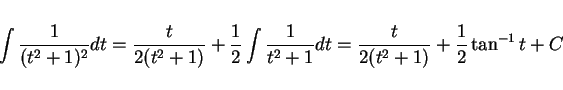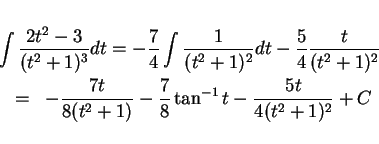

Next: 5 最後に
Up: 4 分子が偶数次の項の場合
Previous: 4.2 4.1
(PDF ファイル: quotef1.pdf)
通常の本でよく取り上げられているのは、多分部分積分で次数を落とす方法
だろうと思われる。これを、前節と同じ
を例に使いながら紹介する。
まず、分子の 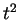 の
の 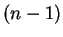 次式を
次式を 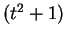 の
の 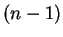 次式に書き直して
(
次式に書き直して
(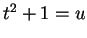 として計算すれば良い)、
として計算すれば良い)、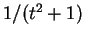 の
の 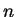 次式の形に書き直す。
次式の形に書き直す。
部分積分を用いて、
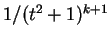 の積分を
の積分を 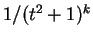 の積分に
帰着させる。
これは、通常
の積分に
帰着させる。
これは、通常
より、
すなわち、
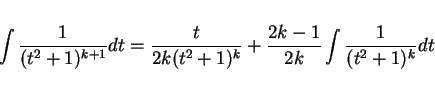 |
(4) |
となる、といったように導かれることが多いようであるが、
これも 4.1 節同様、微分を使って説明することもできる。
となるので、
この両辺を積分して (4) を得る。
今の例では、この公式を使うと (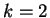 )、
)、
となるので、
であり、もう一度公式を使うと (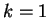 )、
)、
なので、結局
を得る。


Next: 5 最後に
Up: 4 分子が偶数次の項の場合
Previous: 4.2 4.1
Shigeharu TAKENO
2003年 5月 26日
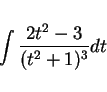
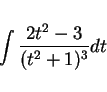
![]() の
の ![]() 次式を
次式を ![]() の
の ![]() 次式に書き直して
(
次式に書き直して
(![]() として計算すれば良い)、
として計算すれば良い)、![]() の
の ![]() 次式の形に書き直す。
次式の形に書き直す。
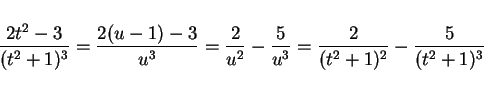
![]() の積分を
の積分を ![]() の積分に
帰着させる。
これは、通常
の積分に
帰着させる。
これは、通常
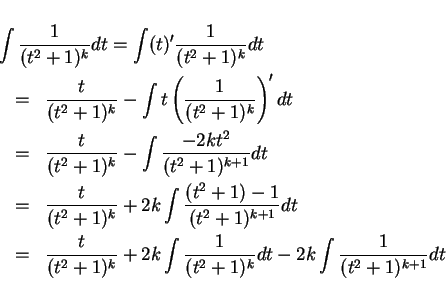
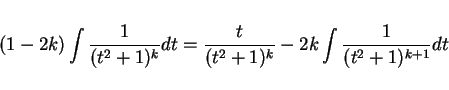
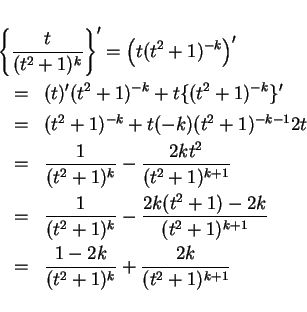
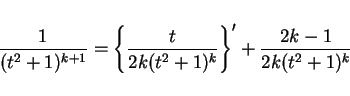
![]() )、
)、