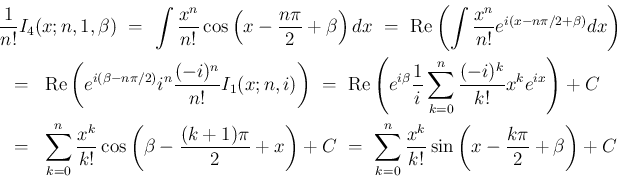4 その他の方法
次は、巾乗と三角関数の積の積分を、
4 節の 2. の方針、
すなわち微分によって求める方法を考える。
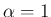 のみ紹介する。
のみ紹介する。
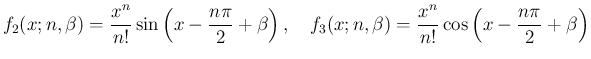
(
21)
とすると、
より、
となり、よって、
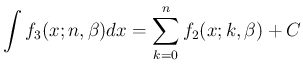
(
22)
となる。これが (19) である。
次は 4 節の 3. の方針、
すなわち複素数を利用する方法も考えておく。
例えば 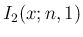 は、
は、
と見ることができる (あるいは
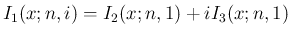 と見てもよい)。
よって、(7) より、
と見てもよい)。
よって、(7) より、
なので、
となり、よってこの実数部分を取れば
となるが、
これは (19) の展開の 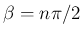 の場合と
同じものであり、すなわち (17) の最初の式を
意味する。
の場合と
同じものであり、すなわち (17) の最初の式を
意味する。
また、
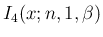 も、複素数を使って、
も、複素数を使って、
のようにして、(7) から (19) を得ることができることがわかる。
竹野茂治@新潟工科大学
2020-03-12
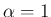
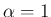 のみ紹介する。
のみ紹介する。
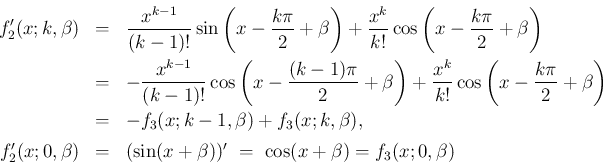
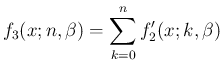
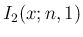 は、
は、
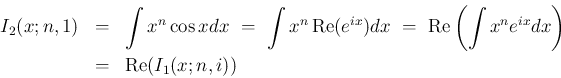
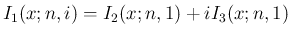 と見てもよい)。
よって、(7) より、
と見てもよい)。
よって、(7) より、
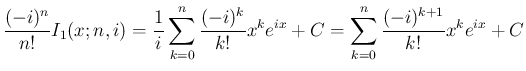
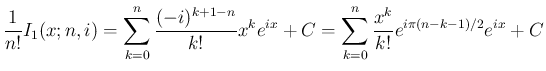
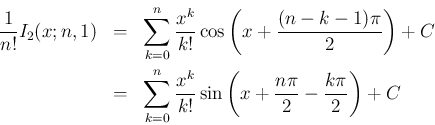
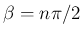 の場合と
同じものであり、すなわち (17) の最初の式を
意味する。
の場合と
同じものであり、すなわち (17) の最初の式を
意味する。
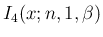 も、複素数を使って、
も、複素数を使って、