3 教科書に出ている公式
次は教科書 [1] に出ている公式 2 の性質について考える。
長所は以下の通りである。
- 長所 1: 公式 1 に比べて計算が 1 手少ない分やさしく、
特に公式 1 の 短所 1 に対する間違いは防げる
- 長所 2: そもそも公式 1 で積の一方を「何かの微分」と書き戻すということは、
そこは 1 回積分していることになるので、
その意味では公式 1 より公式 2 の方が自然である
- 長所 3: 「部分積分」という言葉自体も公式 2 の方が説明しやすい
逆に短所は以下のようなものであろう。
- 短所 1: 公式 2 は対称性がないので覚えにくく、
積の微分とも少し違う形なので、
忘れたときにも思い出しにくい
- 短所 2: 公式 1 より覚えにくいためその点で間違いやすい (右辺の
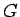 を
を 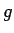 としたり
としたり 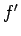 が
が 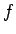 になっていたり)
になっていたり)
公式 2 の長所、短所は、
ほぼ公式 1 の短所、長所と表裏の関係にあるのだが、
少し説明しよう。
まず 長所 1 であるが、
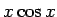 の積分に公式 1 を用いた場合は、
の積分に公式 1 を用いた場合は、
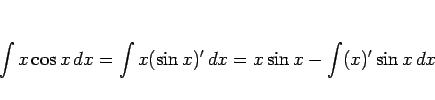
となるが、公式 2 を用いた場合は
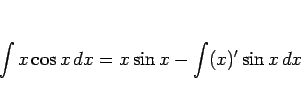
となるので、公式 2 は公式 1 よりも 1 手少なく、
そして 2 節の (1), (2) のような間違いは起こらない。
長所 2 は、
特に 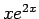 の積分のような場合によくわかる。
公式 1 を用いるなら「
の積分のような場合によくわかる。
公式 1 を用いるなら「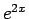 は何の微分であるか」と考え、
は何の微分であるか」と考え、
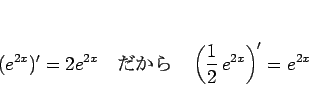
なので、
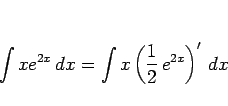
とすることから始めることになる。
しかし、
この「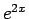 が何の微分であるのか」
と考えることが不慣れな者には苦手なようである。
が何の微分であるのか」
と考えることが不慣れな者には苦手なようである。
一方、公式 2 ならばそうは考えず、
「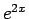 を積分する」と考えるので、直接
を積分する」と考えるので、直接
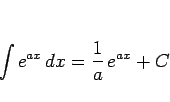
という公式を利用できるのでその点で公式 2 の方がやさしい。
「それが何の微分か」と考えることは「その積分は何か」と同じであり、
むしろ後者の方がストレートでわかりやすいと思う。
長所 3 は、
「部分積分」が英語の「integration by parts」の訳語である通り、
「部分的に一方のみ積分する」ということを指しているわけだから、
その点でも公式 2 の方が自然である、ということである。
ただし、公式 2 を使用した場合も間違いは多い。
典型的には以下のようなものである。
いずれも 短所 2 による間違いであるが、
(7), (9) のような間違いは 公式 1 では起きにくい。
つまり、公式 1 では「積分の中の微分が 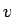 から
から 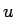 に移る」
と説明できるためにそのように間違えることは少ないのであるが、
公式 2 では右辺に急に微分が出てくるために、
右辺のどこに微分がつくのであったかを間違えることが多いようである。
に移る」
と説明できるためにそのように間違えることは少ないのであるが、
公式 2 では右辺に急に微分が出てくるために、
右辺のどこに微分がつくのであったかを間違えることが多いようである。
また、公式 1 ならば
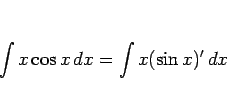
と書いた後は、「右辺には 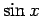 しか表われず、
しか表われず、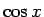 は出てこないはず」
ということを身につければ
(6), (7), (8) のような間違いは起こらない ((2), (3) も)。
これが 2 節の最後に書いた 公式 1 の 長所 2 の利点である。
しかし、これに対し公式 2 は 短所 2 に由来する間違いが起こりやすく、
これを防ぐことは難しく、この点では公式 2 は不利である。
は出てこないはず」
ということを身につければ
(6), (7), (8) のような間違いは起こらない ((2), (3) も)。
これが 2 節の最後に書いた 公式 1 の 長所 2 の利点である。
しかし、これに対し公式 2 は 短所 2 に由来する間違いが起こりやすく、
これを防ぐことは難しく、この点では公式 2 は不利である。
竹野茂治@新潟工科大学
2010年3月16日
![]() の積分に公式 1 を用いた場合は、
の積分に公式 1 を用いた場合は、
![]() の積分のような場合によくわかる。
公式 1 を用いるなら「
の積分のような場合によくわかる。
公式 1 を用いるなら「![]() は何の微分であるか」と考え、
は何の微分であるか」と考え、
![]() を積分する」と考えるので、直接
を積分する」と考えるので、直接