2 通常の公式の性質
まず、公式 1 と公式 2 が同等であるのは明らかだと思うが、
部分積分の公式自体は「積の微分の公式」を積分することで得られる。
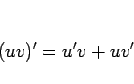
であるから、
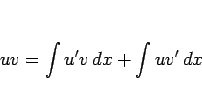
より、右辺の積分を左辺に 1 つ移項すれば公式 1 が得られるわけである。
公式 1 の長所は以下の点であろう。
- 長所 1: 部分積分の証明である積の微分に近い形なので、
公式を忘れたときに思い出しやすい
- 長所 2: 公式 2 よりも間違いにくい点もある
逆に以下のような短所もある。
- 短所 1: 初学者は積の一方を微分の形に一度直してから適用するところがやりにくいらしい (そういう間違いが多い)
- 短所 2: 思い出しやすいとはいっても、やはり公式を間違えて記憶する者も少なくない (真ん中の
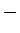 であるとか、微分をつける場所とか)
であるとか、微分をつける場所とか)
公式 1 を使用する場合の典型的な間違いは、
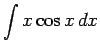 を例にとれば以下のようなものである。
を例にとれば以下のようなものである。
(1) から (4) は公式の記憶ミスや使い方のミスで、
(1), (2) は 短所 1 によるもの、
(3), (4) は 短所 2 による間違いである。
(5) は計算自体に間違いはないが、方針のミスである。
この 短所 1 による間違いは、
教科書 [1] に載っている例が
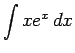 であることにも原因があるように思う。
であることにも原因があるように思う。
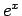 は微分も積分も
は微分も積分も 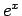 だから、
その例で部分積分の公式を理解しようとする学生は (1), (2) のようにしてよい、
と考えた可能性はある。
だから、
その例で部分積分の公式を理解しようとする学生は (1), (2) のようにしてよい、
と考えた可能性はある。
もちろん、講義ではそのような勘違いが起きないように、
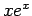 ではなく上の
ではなく上の 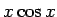 の積分で説明をしているのであるが、
それでもこのような間違いがでるところを見ると、学生は、
の積分で説明をしているのであるが、
それでもこのような間違いがでるところを見ると、学生は、
- 普段の講義をほとんど聞いておらず (ノートも取らず)、
試験前に初めて勉強しだす
- ノートは取るものの、ノートよりも教科書を信用する
という状況なのかもしれないが、
このような間違いが必ずある割合は出てくるように思う。
最近、どうせ公式の記憶違いをするのであれば、
短所 2 よりも多分ハードルが高いと思われる 短所 1 を解消できる公式 2 の方がいいのでは、
と思うようになってきた。
しかし、公式 1 もちゃんと使えるようになると、
長所 2 に書いたように公式 2 よりも間違いにくいところもある。
これは、3 節で説明しよう。
竹野茂治@新潟工科大学
2010年3月16日
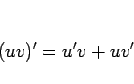
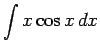 を例にとれば以下のようなものである。
を例にとれば以下のようなものである。
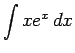 であることにも原因があるように思う。
であることにも原因があるように思う。
![]() は微分も積分も
は微分も積分も ![]() だから、
その例で部分積分の公式を理解しようとする学生は (1), (2) のようにしてよい、
と考えた可能性はある。
だから、
その例で部分積分の公式を理解しようとする学生は (1), (2) のようにしてよい、
と考えた可能性はある。
![]() ではなく上の
ではなく上の ![]() の積分で説明をしているのであるが、
それでもこのような間違いがでるところを見ると、学生は、
の積分で説明をしているのであるが、
それでもこのような間違いがでるところを見ると、学生は、