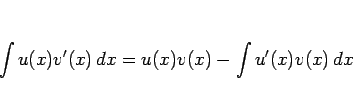1 はじめに
部分積分の公式というと、大学向け、高校向けのどの教科書も、
次の形で書かれているものが多いと思う。
公式 1:
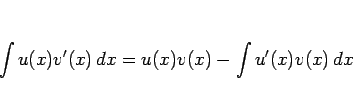
もちろん、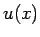 ,
, 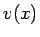 を逆にした形のものはあるものの、
普通この形以外のものを見ることはほとんどないし、
私自身この形で学び、この形で使ってきた。
を逆にした形のものはあるものの、
普通この形以外のものを見ることはほとんどないし、
私自身この形で学び、この形で使ってきた。
しかし、現在基礎数理で使用している教科書 [1] は、
部分積分の公式を次の形で書いている。
公式 2:
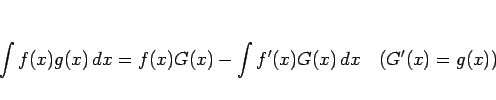
これは、公式 1 の 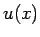 を
を 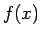 、
、
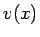 を
を 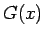 と見た形をしている。
と見た形をしている。
一般的には公式 1 が使われることや、
高校の教科書でもそれで書いていることから、
以前は講義では教科書とは別に公式 1 の形で教えていたが、
数年前から 公式 1、公式 2 の両方を紹介し、
- 公式 1 はどちらかというと標準的である
- 公式 2 は、公式 1 よりも計算が少しやさしい
という形で教えている。
本稿では、この両者の長所、短所を比較し、それらについて考察し、
その他の方法についても少し考えてみたいと思う。
竹野茂治@新潟工科大学
2010年3月16日