4 微分の公式の証明
無限小の方法を用いた場合、積の微分の公式の「証明」は以下のようになる。
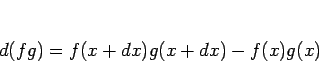
であり、
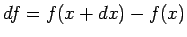 より
より
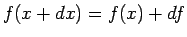 なので、
なので、
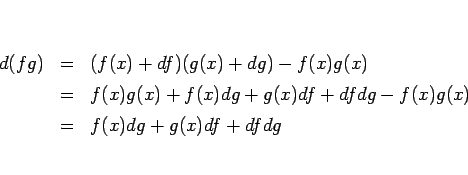
となるが、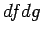 は
は 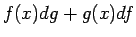 より高位の無限小なので無視すれば、
より高位の無限小なので無視すれば、
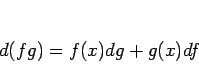
となる。よって、
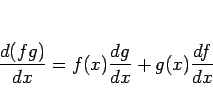
となる、といった形になる。
この証明は、2 節の最後に上げた方法と本質的に
同じであることがわかるだろう。
しかも展開により自然に積の微分の形が得られていることや、
最後の 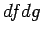 が消える理由も、
むしろこちらの方がわかりやすく感じる人もいるかもしれない。
が消える理由も、
むしろこちらの方がわかりやすく感じる人もいるかもしれない。
なお、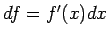 であることに注意すれば、上の変形は、
であることに注意すれば、上の変形は、
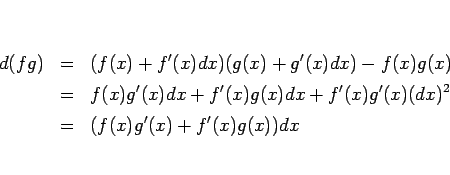
のようにして (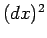 は高位なので無視している)、
両辺を
は高位なので無視している)、
両辺を 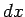 で割る、とすることもできる。
で割る、とすることもできる。
同様に、商の微分の公式も以下のようにできる。
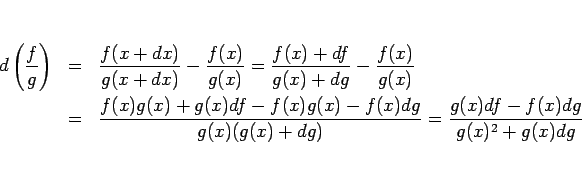
この分母の 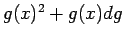 では
では 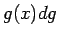 は無限小なので
は無限小なので 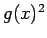 に
対して無視できるから、
に
対して無視できるから、
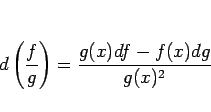
となり、よって両辺を 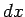 で割れば、
で割れば、
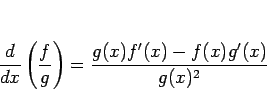
となる。
合成関数 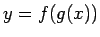 の微分の公式も、
の微分の公式も、
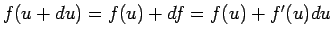 を用いれば、
を用いれば、
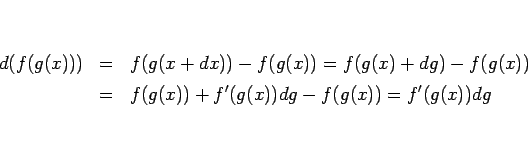
となり、よって、
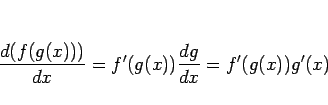
が得られる。
竹野茂治@新潟工科大学
2015年12月7日
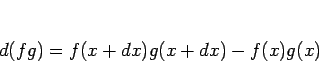
![]() が消える理由も、
むしろこちらの方がわかりやすく感じる人もいるかもしれない。
が消える理由も、
むしろこちらの方がわかりやすく感じる人もいるかもしれない。
![]() であることに注意すれば、上の変形は、
であることに注意すれば、上の変形は、
![]() の微分の公式も、
の微分の公式も、
![]() を用いれば、
を用いれば、