(07/15 2001)
期末試験の採点をしていて、気になった誤答等がありました。 小テストに関しては講義中に指摘しましたが、 期末テストに関しては話す機会がありませんので、 ここにまとめておきます。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
基礎数理 II は、現在 (2009) は基礎数理 I の続きの微積分をやっているのですが、 基礎数理 I と II ではクラス分けが異なる (I は 3 クラス、II は 2 クラス) ため、 基礎数理 I の B クラスだった学生が基礎数理 II の B クラスに来ると 最初とまどう、という話を例年聞いていました。
授業が進むとあまり問題はないようなのですが、 今年 (2009) は試みとして、希望者に 3 回だけ演習形式で 基礎数理 I C クラスの内容の補習を行いました。 学生の参考になるかもしれませんので、その配布資料をここに置きます。
教科書に、定積分による置換積分、部分積分の公式がのっていますが、 講義中に注意したようにその運用にはミスが多いようです。よって、 置換積分、部分積分は定積分では行わず、不定積分でのみ使用して、 そこで求めた原始関数を利用して定積分の値を計算する、という方法を 講義では紹介しました。
その後、もう一つ別な工夫を思いつきました。この方法の方が、 その運用には誤解が少なくなるような気がします。 また、定積分と不定積分自身の違いもより明確になるのではないかと思いますので、 それをここに紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
リーマン和の極限で定積分を定義する区分求積法を講義中で紹介しましたが、 極限として面積になる、というところは実際には多少ごまかしがあります。 つまり、リーマン和はあくまで面積の近似でしかなく、その極限を取ると、 その誤差が 0 に収束するということを、本当は証明する必要があります。
連続関数のグラフに対しては、それが証明できるのですが、教科書には その証明は書いてありません (定理 12.2)。 それは、一般の連続関数に対してそれを証明するには、他にまだいくつかの 事柄 (例えば極限や連続性の厳密な定義、連続関数の一様連続性という性質など) が必要になるからです。
しかし、f(x) が微分可能で、f'(x) も連続であるような場合には多少簡単に (とはいっても十分面倒ですが) それを説明できますので、ここで紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
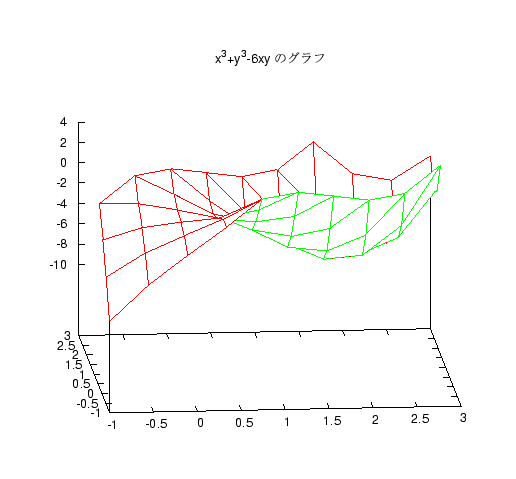
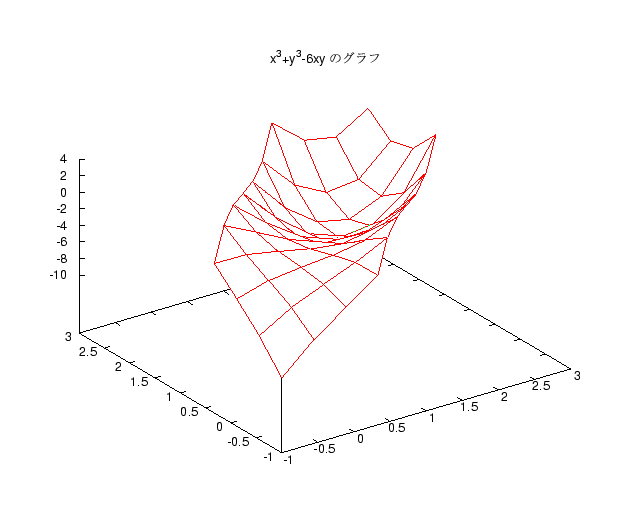
講義中に 2 変数関数の極大極小の問題として、 z=x3+y3-6xy を取り上げ、 そのグラフも紹介しましたが、グラフは多分見えにくかっただろうと思います。 よって以下にそのグラフを置いておきますのでご覧ください。
(07/15 2001)
後期試験、木曜 5 限の方 (情報電子) では次のような立体の体積を求める問題を 出しました。
高さ 10 の立体があり、高さ x でのその立体の水平断面が、 一辺の長さが \(2(10-x)^{1/3}\) の正方形であるとき、 この立体の体積を求めよ。そのような立体は色々考えられますが、まず 2 つの例をグラフで紹介します。
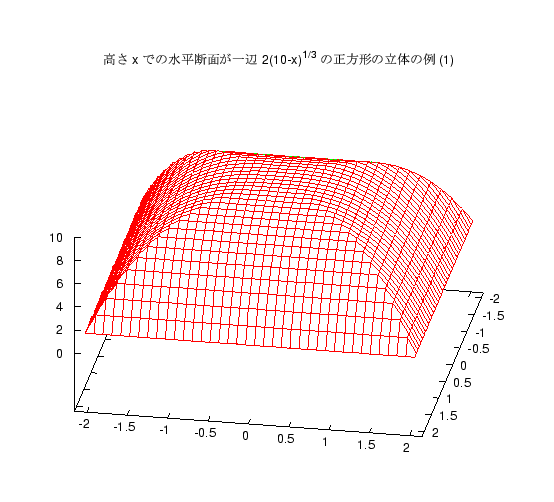
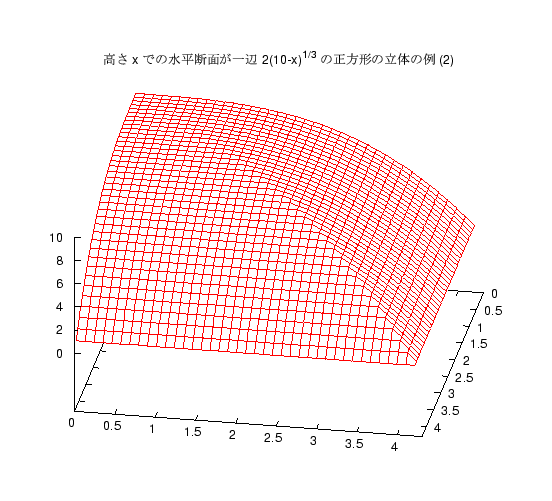
答案に図形を書いている人もいましたが、 残念ながらこれに似た形の立体はほとんどなく、 直方体、あるいはそれが多少ゆがんだものを書いている人が多かったようです。 頂上 (x=10) では明らかに断面積 0 なのですが、 それには気がついた人はわずかしかいませんでした。
上の 2 つの立体は、各断面の正方形を中心に置くか、端に置くかの違いですが、 これをねじったものも題意を満たす立体になります。 これに気がついてねじった図を答案に書いた人もいましたが、 やってみるとわかりますが、 ねじる角度が大きいと途中の面が底面をはみ出る図形になります。 そのような図形を紹介します。
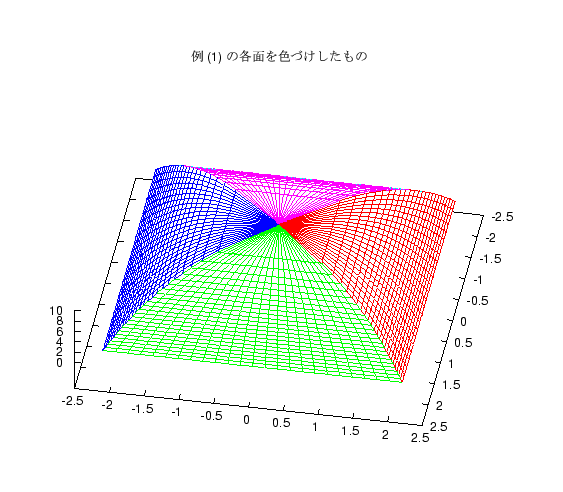
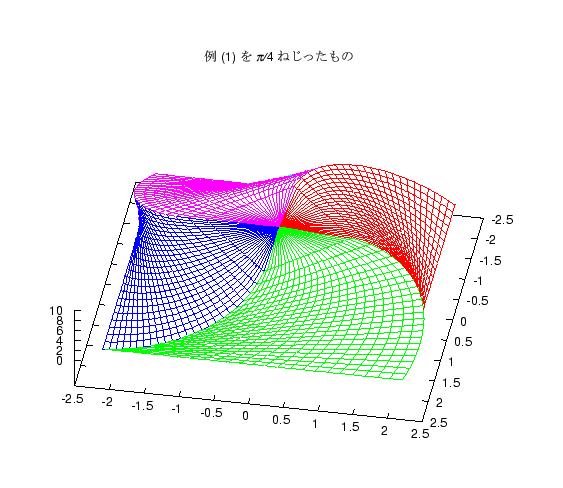
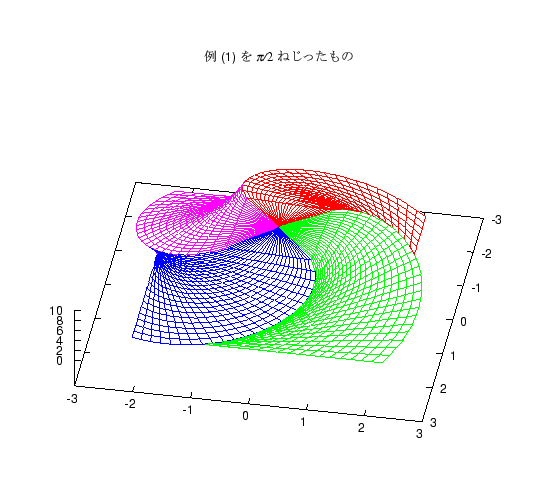
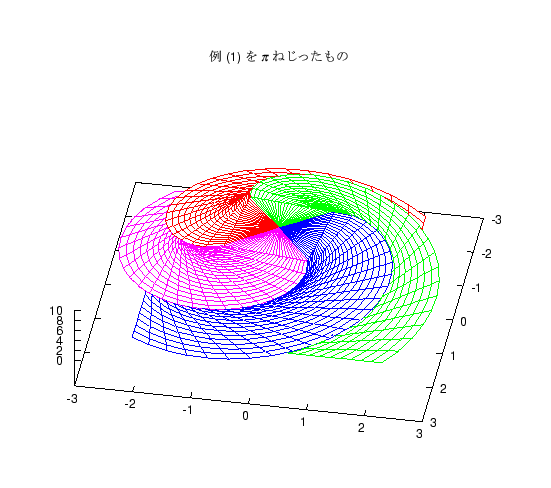
(07/29 2001)
毎年偏微分の合成関数の微分法の所になると、 教科書には載っていませんが x の x 乗の微分の例を紹介しています。 これは最初の年の学生から教えてもらった話を元にしたものです。
ついでにその極限である "0 の 0 乗" の話を追加して ここに紹介することにします。
なお、少し誤解を受けそうな箇所があったので、追記を加えました (03/05 2006)。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
毎年有理関数の積分に関して部分分数分解による方法を紹介していますが、 そこに出て来る一番難しい形のものの積分は 時間の都合上易しいもののみを説明をし、 一般的なものの説明は省略することが多いので、 一般的なものも含んだ説明をここで紹介しておきます。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
これに加えて、実際の計算のしやすさを、もう少し考えてみました。 これも紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
教科書には書いてありませんが、 例年講義で紹介している「部分分数分解の原理」の証明も書いてみましたので これも紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
一番難しい形の有理関数に関しては、 複素数を利用した部分分数分解でやる、 という方針も立つのですが、実はそれはそんなに簡単ではありません。 これについても少しまとめてみましたのでここに紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
上では、複素数を使って部分分数分解する方法を一部紹介していますが、 1/(x+i), 1/(x-i) の積分は、複素対数を使うことを避け、 それをまた通分して a/(x2+1) の形に戻して積分しています。 これを通分せずに複素対数を使って考えてみたものを以下に紹介します。
なお、tan x/2=u の置換積分を使う 1/(2 + cos x) の不定積分も、 複素数を使って考えてみるとやはり複素対数が出てきます。 これも合わせて紹介します。通常、整式の商の部分分数分解は、 「部分分数分解の原理」 に基づいて、 最終的な形の分子を未定係数で表現して、 それが恒等式として満たされるようにその未定係数を決定する、 という方法を取ります。
それに対して、未定係数によらない方法での部分分数分解、 というものを考えてみましたのでここにまとめておきます。
積分の定義のところで区分求積の話をしていますが、 これを利用すると、無限級数 \[ 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots \] の値を求めることができます。 初等的な計算のみでできますので、 その計算をここで紹介します。
ただし、「区分求積」の例として適切なものだとはいえないでしょう。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
高次導関数に対する積の微分の公式として「ライプニッツの公式」と 呼ばれるものがあります。 これは、範囲としては基礎数理 I で履習する範囲のものですが、 偏微分を使う証明で、通常の証明 (帰納法) よりも よりこの公式の意味を説明するようなものを考えましたので、 ここにまとめておきます。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
直接基礎数理 III とは関係はありませんが、 数学には、色んな場面で「n 次元球 (2 次元の円、3 次元の球の拡張) の体積」が出てきます。 それは、大学の多変数の積分の演習問題として扱われることが多いのですが、 対称性を利用して多少おおざっぱな考察をすれば 、 1 次元の定積分で計算できなくはありません。
それには、cosθ の n 乗の定積分の計算 (部分積分) なども出てきて、 基礎数理 III の応用にもなると思いますので、 この計算を実際にやってみた例をここにまとめておきます。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
以前、ある大学院生に次のような質問をされたことがあります。
マイコンに勾配 (タンジェント) の値からその角度を求める プログラムを載せようと思っているが、 アークタンジェントのマクローリン展開を 使うと誤差が大きくなってしまうのだがどうしたらよいか。元々マクローリン展開は x=0 での展開式なので |x| の値が大きい場合はその誤差が大きくなってしまいます。 しかしうまく工夫すれば、そのマクローリン展開でも ある程度の精度で計算できます。 それについてここにまとめておきます。
ジェットコースターのようにくねくねと変化する曲線上を質量のある物体をすべらすと、 その上に凸な部分で速度が出すぎるとその曲線を離れ得ます。
それが起こるための曲線と速度との関係を、 テイラー展開を用いて求める方法を思いついたので、 それをここにまとめておきます。
道路のカーブの曲がり具合を表すのに、R=200 のように表現することがありますが、 それは「円で言えばその半径が 200m くらいの曲がり具合である」という意味です。
一般の曲線に対しても、実際にはそれが円の一部ではなくても、 円で言えばそれがどれくらいの半径の曲がり具合であるか、 ということを表現する 曲率半径 と呼ばれるものがあります。 工学では出てくる場面は多少ありそうな気がしますが、 本学 1,2 年生の微積分の教科書には書かれていないようなので、 どのようにしてそれが得られるのかをここにまとめておきます。
\(\cos^mx\sin^n x\) (m, n は 0 以上の整数) の不定積分の計算はよくある問題ですが、 基礎数理 II で使用している教科書には書いてなかったので、 今年度 (2009) の宿題の解答として配布した手書きのプリントの余白に、 余談としてその積分方法を何通りか紹介しました。
せっかくなので、省略した部分も加筆して、 ここにそれをまとめておきます。
部分積分の公式というと、大学向け、高校向けのどの教科書も、
公式 1: \(\displaystyle\int u(x)v'(x)dx = u(x)v(x) - \int u'(x)v(x)dx\)の形で書いているものが多いのですが、 現在基礎数理で使用している教科書では、
公式 2: \(\displaystyle\int f(x)g(x)dx = f(x)G(x) - \int f'(x)G(x)dx \ \ (G'(x)=g(x))\)と書いてあります。これは公式 1 の u(x) を f(x)、 v(x) を G(x) と見た形になっています。
これらも含めて、その他の方法についても少し考察してみましたので、 ここにそれをまとめておきます。
双曲線関数は、三角関数と似た記号を使って書かれるものですが、 実際には指数関数の簡単な式で定義される関数なので、 特に新しい関数として追加されるようなものではなく、 よって数学の教科書でも定義とそのグラフ程度しか紹介されないことが多いようです。
実際、基礎数理の教科書でも、 定義と簡単な性質が発展として 1 頁書かれているだけです。
そこで、せっかくですから、 この関数の他の性質などを、余談も含め色々調べてみましたので、 ここにそれをまとめておきます。
現在は、微分の定義は通常極限を用いて行われていて、 導関数の公式も原則極限を用いて証明されています。 よって「dy/dx」は、 一応は「Δy/Δx」の極限、という意味は持っていますが、 「dy ÷ dx」という分数の意味は持たず、 「y を x で微分したもの」と見ることになっています。
しかし、合成関数の微分や逆関数の微分の公式では「dy/dx」の 分数らしい性質がでてきますし、 置換積分では、「dy=f'(x)dx」のような、 「dy/dx=f'(x)」の左辺を分数と見た式も使われていますし、 工学の本や海外の本では 「dx」のような「無限小」を利用する計算は 今でも使われている場合もあります。 そして、そのような計算の方が説明がわかりやすく見えることもあります。
よって、現在では厳密な議論ではないということで 「無限小」による説明は排斥されがちなのですが、 それを紹介することも多少は意味があるのではと考え、 ここにまとめておきます。
三角関数の導関数の公式の証明は、 \(\sin x/x\) の極限に基づくものが多いのですが、 図形的な説明を以前以下に書きました。
それは、「図形的」とはいいつつ、やはり \(\Delta\sin x/\Delta x\) の極限を図形的に考えるものです。
一方で、三角関数のグラフを、 透明なフィルムによる円筒を使って見ることができることを 基礎数理 I で紹介しました。
その手法を使って三角関数の導関数の公式を求める方法もあります。 以下にその説明がありますので紹介しておきます。
部分積分が適用できる関数の例として 数学の教科書で良く取り上げられるものに、 多項式と指数関数の積の積分と、多項式と三角関数の積の積分があります。
これらは、1 回部分積分を行うことにより、 次数が 1 つ小さい多項式の積の積分に帰着できるため、 その多項式が定数になるまで部分積分を繰り返せば、 いずれ積分が終了しますが、 教科書などではその原理的な方法のみが紹介され、 最終結果の式はでてきませんので、 部分積分によって漸化式を導くことで、 \(x^n\) と指数関数の積、 \(x^n\) と三角関数の積の積分の 具体的な表現式の作成について考察してみましたので、 ここにまとめておきます。
以前、「無限小による微分の公式の証明」 で、 無限小を用いて積の微分、商の微分の証明などを書きました。 そこで紹介した商の微分の証明以外にも商の微分の証明はあるので、 それをここにまとめておきます。
以前、「商の微分について」 で 商の微分の証明をいくつか紹介しました。 今度は、積の微分の証明を 2,3 紹介します。
ここでは、講義では触れなかった、合成関数の微分に関する以下の補足を 2 つまとめておきます。
講義で使用している教科書では、指数関数に関するある補題 (教科書の (1.1)) \[ \lim_{x\rightarrow\pm\infty}\left(1+\frac{1}{x}\right)^x=e \] の証明を省略する、としているので、 ここでその証明を紹介しておきます。
以前、「基礎数理 I」 のページに、 「微分して元に戻る関数について」 という記事を書き、そこでは 1 回、2 回、4 回微分して元に戻る関数を紹介しました。
その話は、現在は基礎数理 II(b) でしていて、 さらに基礎数理 II(b) では授業中に『じゃあ 3 回微分して元に戻る関数は ?』 と話していますが、その答は示していませんでした。
上に紹介した 「微分して元に戻る関数について」 でも、 『3 回微分して元に戻るものを求めるのは少し難しい』と書いていて、 それ自体は紹介していませんでした。
ということで、3 回微分して元に戻る関数、 および一般の n 回微分して元に戻る関数についてまとめてみましたので、 それをここに置きます。
なお、これは、 「微分して元に戻る関数について」 をベースに書いていますので、 まずはそちらを先に読むといいでしょう。
教科書 3 ページに関数に対する「増加」「減少」「単調」という 用語の説明が書いてあります。 そしてさらに「単調増加」「単調減少」という用語もあります。 それについて少し補足説明をします。 なお、細かい話なので、あまり気にする必要はありません。
関数の「増加」や「単調増加」といったものには、実は 2 種類あります。 最も細かく言えば、それは「狭義単調増加」と「広義単調増加」という言葉で 規程されるものです。以下、f(x) の定義域を I とします。
[A],[B] の違いは、f の不等式に等号が入るか入らないかですが、 この定義からすると、[B] は定数関数、 または I の部分区間で定数になっている関数も含みますが、 [A] はそういう関数は含みません。 しかし、いずれも \(f(x)=x^3\) のように、 ある点で f'(x)=0 となっているがそれ以外では増加する関数は含みます。
で、ややこしいのはその呼び名なのですが、 上のように「狭義単調増加」や「広義単調増加」は長いので、 そう呼んでいる本は多くなく、例えば [A] は「増加関数」、 [B] は「単調増加関数」のような使い分けで済ましている本が多いようです。 その場合「単調増加関数」が「増加関数」を含むことになりますが、 「単調増加関数」は「増加関数」の特別な場合と誤解しやすいので注意が必要です。
講義で使用している教科書は、「単調増加」という言葉は使っておらず、 [A] を「増加関数」と呼んでいて、 [B] の概念の名前付けはしていないようです。
(09/26 2022)教科書 4 ページの公式 1.1 の証明は書いてありませんが、 それについて補足します。なお、細かい話なので、気にする必要はありません。
公式 1.1 の証明は書いてないのは、 この教科書では「極限」自体の厳密な定義が書かれていないためで、 ある意味当然です。 この教科書では極限は、「x が a に限りなく近づくときに関数 f(x) が限りなく近づく値」のように説明していますが、 この「限りなく近づく」とはどういうことかが示されておらず、 厳密な数学的な定義にはなっていません。
極限の厳密な定義は少し面倒で、 歴史的にもその厳密な定義が作られるまではやや時間がかかり、 現在はフランスの数学者コーシー (A.L.Cauchy 1789-1857) の提示した、 「ε-δ論法」が広くその定義として使われています。 しかしこのε-δ論法は結構厄介なので、 工学部の微積分の教科書には書かれていないことも多いですが、 このような定義を導入しないと公式 1.1 は証明できません。
なお、「ε-δ論法」は極限を厳密に定義するだけのもので、 これを知っても計算が楽になるとか、 理屈がわかりやすくなるものではありませんので、 知る必要はありませんが、もし知りたい場合は、例えば以下を参照してください。
(09/26 2022)極限に関連して、「数学では 0 では割り算できない」という話をしましたが、 あらためて説明しておきます。
割り算
x ÷ y = z ... (1)は、かけ算
y × z = x ... (2)の逆として定義されます。 つまり x ÷ y の答えとは、 y に何かをかけたら x になるようなものです。
そして「0 では割り算ができない」という話は、 (1) で y = 0 の場合は、そのような z は、 実数には存在しないか、または一つには決まらない、 ということになるために 「0 では割り算ができない」ということになっています。 そのことを以下に示してみます。
まず、x が 0 でなく、y = 0 の場合の x ÷ 0 = z となる z を考えてみます。 この場合、(2) は 0 × z = x なので 0 = x となってしまい、これは x が 0 でないことに矛盾します。 よって、(2) となるような z、すなわち x ÷ 0 = z となる z は存在しません。
次に、x = 0 で、かつ y = 0 の場合の 0 ÷ 0 = z となる z を考えてみます。 この場合、(2) は
0 × z = 0 ... (3)となるので、0 = 0 となり、矛盾ではありません。 しかし、(3) を満たす z は一つに決まらず、 z がどんな実数であっても (3) は成立してしまうので、 よってこの場合は z が一つに決まりません。
以上により、0 でない x に対しては x ÷ 0 は存在せず、 0 ÷ 0 は一つに決まらないので、 「0 での割り算はできない」ということになっています。
(10/03 2022)片側極限の記号は、講義では 「\( \displaystyle\lim_{x\rightarrow a+0}f(x)\)」, 「\( \displaystyle\lim_{x\rightarrow a-0}f(x)\)」 という記号を紹介しましたが、 本によっては他の書き方もあります。それをいくつか紹介します。 なお、この授業では、講義で指示した書き方を使用してください。
講義ではほぼ説明を省略しましたが、 「\( \displaystyle\lim_{x\rightarrow a}f(x)=f(a)\)」 となる場合、f(x) は x=a で「連続」であるといい、 f(x) の定義域のすべての x で連続な場合は「連続関数」 と言います。 ただし、定義域が I=[a,b] のように端が含まれている区間の場合は、 x=a, x=b での連続性は、片側連続性、すなわち 「\( \displaystyle\lim_{x\rightarrow a+0}f(x)=f(a)\)」、 「\( \displaystyle\lim_{x\rightarrow b-0}f(x)=f(a)\)」で置き換えます。
連続関数は、定理 1.3, 1.4 のように、定義域内の有限な閉区間に対して、 最大値・最小値の存在、中間値の存在が保証されます。 連続関数でない場合はその存在は一般には保証されません。 この定理を利用すると、例えば以下のようなことが証明できます。
また「連続性」は一見わかりにくいものもあります。 例えば当然次のような関数 f(x) は、 どんな x=a に対しても連続ではありません。
f(x) = 0 (x が無理数のとき)、ところが、次のような関数 g(x) は、 有理数の a では連続ではありませんが、 無理数の a では連続となります。
f(x) = 1 (x が有理数のとき)
g(x) = 0 (x が無理数のとき)、既約分数とは、もう約分ができない分数のことを言います。有理数は、 分母が正の既約分数の形に一意的に表すことができますので、 この関数もすべての x に対して値が正しく定まります。 しかし、無理数の a では連続となること、 すなわち 「\( \displaystyle\lim_{x\rightarrow a}g(x)=g(a)=0\)」 となることが納得できるでしょうか (証明は少し面倒)。 (10/04 2022)
g(x) = 1/q (x が有理数、x=p/q (q>0) が 既約分数のとき)
講義で紹介しなかった逆三角関数の性質を、以下にまとめておきます。
以前、合成関数の微分に関する補足として、 「合成関数の微分に関する補足」 でその公式のラフな証明、すなわち高校の教科書で良く紹介されいている証明と、 合成関数らしいがそうではない関数の微分の方法を紹介しました。
講義で使用している教科書の今の版では、 そのラフな証明の問題点もクリアにするものが付録に書かれていますが、 少しわかりにくいところもあるので、 その証明を少しわかりやすくしたものを以下に置きます。
また、教科書の証明は、実は普通の解析の本に書いてある証明とは 少し違っていて、場合分けを行う証明なのですが、 良く見られる場合分けによらない証明も紹介します。
第 5 回の復習問題で出した、雪玉の問題について、 気がついたことと補足について、ここにまとめておきます。
講義では指数関数・対数関数の微分の公式の証明は省略しましたが、 教科書とは別の証明も含め、ここにまとめておきます。
講義の「逆三角関数」のあたりで、逆関数について簡単に説明しましたが、 逆関数の例 (講義でもいくつかは紹介しました) をいくつか上げておきます
最後のいくつかの例のように、計器には、そのものを直接計るのでなく、 それとともに変化して数字に変えることのできるものを計測して、 その逆関数として元々計りたいものを計る、 という仕組みのものがいくつもあります。 他にも何か思いついたら追加しておきます。
(11/24 2022)基礎数理 II の講義の複素数のところで、以下の事実を紹介しました。
それについて、少し余談を紹介します。
3 次方程式の解の公式 (解法) については、Wikipedia ででも見つかりますが、 現在「カルダノ」の解法と呼ばれている方法は、 実はジロラモ・カルダノ (1501-1576 イタリア) が発見したものではなく、 ニコロ・フォンタナ (1500?-1557 イタリア) が見つけたもので、 それをカルダノが口外しないことを条件に聞きだした末に 自分の著書の中で発表したものです。 当時イタリアでは、数学の勝負が流行っていて、 その主要な問題が 3 次方程式だったそうです。
4 次方程式は、カルダノの弟子のロドビコ・フェラーリ (1522-1565 イタリア) が、3 次方程式を利用して解く方法を見つけました。 10 代の頃の発見と言われています。
その後、5 次方程式の解の公式を見つける努力が多くの人によって行われましたが、 それはかなわず、最終的にニールス・アーベル (1802-1829 ノルウェー) が 22 才のときに、 累乗根を使って 5 次方程式の解を表す公式を作ることはできない、 ということを証明し、この問題に終止符が打たれ、 さらに累乗根で代数方程式が解けるための必要十分条件が、 エバリスト・ガロア (1811-1832 フランス) によって発見されました。
しかし生没年を見るとわかりますが、 フェラーリもアーベルもガロアも長生きはしていません。 フェラーリは数学勝負で有名になって、大学教授にもなり、 財産も蓄えますが、43 才のときに姉 (か妹) に毒殺されたと言われていて、 フェラーリの遺産を相続した姉 (か妹) も、 その後すぐに結婚した相手に遺産を持ち逃げされたと言われています。
アーベルは大学に職を望みましたがかなわず 26 才で病死、 ガロアは学生時代に政治運動にのめりこみ、何度も投獄され、 最後は 20 才で決闘で亡くなっています。 アーベルとガロアの業績が評価されたのは、いずれも亡くなった後のことです。
これは「代数学の基本定理」と呼ばれるもので、 2 次方程式で複素数が必要になりますが、 3 次以上の方程式でも複素数以上に数を広げる必要はなく、 複素数の範囲で n 次方程式 (正確には、実数係数、または複素数係数の n 次方程式) が n 個の解を持つ、 言いかえれば n 次式が複素数を用いて n 個の一次式の積に因数分解できる、ということが証明されています。
証明したのは 19 世紀最大の数学者と言われるカール・フリードリッヒ・ガウス (1777-1855 ドイツ) で、22 才のときに提出した博士論文に書かれています。
なお、ここでいう「n 個の解が存在すること」と 「5 次方程式の解の公式がないこと」は矛盾するわけではありません。 アーベルが証明したのは、「累乗根で 5 次方程式の解の公式が作れない」 ということで、累乗根以外を使えば解法は存在する可能性があります。
逆にガウスは、必ず複素数の中に n 個の解が存在することは示したのですが、 それを具体的に方程式の係数を用いて表す解の公式を作ったわけではなく、 「存在すること」を証明しただけです。
ここに出てくるいずれも天才的な数学者ばかりですが、 4 次以上の方程式に関する業績が、 すべてごく若い世代 (10 代から 20 代前半) に固まっていることも、なんとなく興味深く感じます。
(12/27 2022)基礎数理 II の講義では、 積分に「不定積分」「定積分」の 2 種類があることを紹介しましたが、 他にも「積分」がつく用語はたくさんあります。 それらについて、いくつか紹介しておきます。
xy 平面上の領域 D 上で定義された関数 f(x,y) の積分、 すなわち関数値 f(x,y) と微小面積 dxdy の積の総和で、 z=f(x,y) のグラフの曲面と xy 平面が D 上で囲む立体の体積となる (xy 平面の下は負とみなす)。 基礎数理 III で学習する。
3 次元空間内の 3 次元領域 V 上で定義された関数 f(x,y,z) の積分、 すなわち関数値 f(x,y,z) と微小体積 dxdydz の積の総和。
3 次元空間内 (または 2 次元平面上) の曲線 C に沿って 関数 f を積分したもの。\(\int_C fds\) の場合は、 f の値と曲線の微小な長さ ds の積の C に沿っての総和、 \(\int_C fd\vec{r}\) の場合は、 f の値と曲線の微小な接ベクトル \(d\vec{r}\) の積の総和。
3 次元空間内の曲面 S 上での、関数値 f(x,y,z) と曲面の微小面積 dS の積の総和。
V 上の三重積分と同じ。
複素変数の関数 f(z) の、複素数平面上の曲線 C に対する線積分。
最も標準的な定積分の定義。x 軸上の有限な区間 I=[a,b] と、その上で定義された有界な関数 f(x) に対して、 I を小さい区間 \(a=x_0 < x_1 < x_2 < \cdots < x_n=b\) に分割し、 各小区間 \([x_{k-1},x_k]\) では面積を長方形 \(f(c_k)\Delta x_k\) (\(x_{k-1}\leq c_k\leq x_k\), \(\Delta x_k = x_k - x_{k-1}\)) で近似したものの総和 (= リーマン和) \(\displaystyle\sum_{k=1}^n f(c_k)\Delta x_k\) の \(n\rightarrow\infty\) のときの極限として定義される定積分。 いわゆる区分求積法。
リーマン積分が面積を縦に細分して近似するのに対し、横に近似する方法、 すなわち関数の値の方を離散化して、その値で関数を階段関数 (単関数) で近似して、その面積の極限で定積分を定義したもの。 単関数の段階で x 方向の分割が無限個となりうるため、 「幅」の計算のために「測度」の概念が必要になり、 関数の極限や無限和、無限に長い範囲の積分によくなじむ。
リーマン積分では、定積分は関数 f(x) の値と x の微小変化 dx の積の総和を考えるが、 dx の代わりに別な関数 g(x) の微小変化 dg = g(x+dx)-g(x) との積の総和を考えたもの \(\displaystyle \int_a^b f(x)dg(x)\)。
リーマン積分流の定義によるリーマン−スティルチェス積分、 ルベーグ積分流の定義によるルベーグ−スティルチェス積分がある。 確率論や統計学で利用されることが多い (多分)。
通常のリーマン積分は、有限な区間上の有界な関数に対する定積分だが、 それを、リーマン積分の極限を用いて、 無限な区間の定積分、あるいは有界でない関数に対する定積分に拡張したもの。
ルベーグ積分は通常は最初から無限な区間、有界でない関数に対する定積分だが、 その値はリーマン広義積分に一致する場合もあるし、一致しない場合もある。
積の微分の公式の逆として得られる積分公式。 積の積分や、対数関数の含まれる積分などのある種の積分が これにより多少簡単になることがある。 なお、積の積分がこれにより常に積分できるようになるわけではない。
合成関数の微分の公式の逆として得られる積分公式。 合成関数の含まれる積分や、 ある種の積分がこれにより多少簡単になることがある。 なお、合成関数の積分がこれにより常に積分できるようになるわけではない。
一般に定積分の近似値を求める方法を指す。主にコンピュータを使用する。 台形公式、方形公式、シンプソンの公式などが良く知られている。
\(\int_0^\infty f(x)\sin tx dx\) \(\int_0^\infty f(x)\cos tx dx\) のように、 三角関数との積の定積分によって得られる t の関数を指す。 いわゆるフーリエ変換の一部。
\(\int_0^x\sin(t^2)dt\), \(\int_0^x\cos(t^2)dt\) の形の積分。 初等関数で表すことはできない。光学や道路工学 (クロソイド曲線) などで用いられる。
元は楕円の周の長さを求めるための定積分。 円以外の場合は初等関数で表すことはできない。 そこから発展して、同様の形の定積分 (三次式や四次式の平方根が含まれる積分) も「楕円積分」と呼び、種々の標準形が得られている。
オイラーの公式
\( e^{\theta i}=\cos\theta+i\sin\theta \)は、「公式」というよりも新たな虚数乗の「定義」なのですが、 こう定義するのが自然であるという状況証拠はいくつかあります。 そのいくつかをここで紹介します。
講義でも紹介しましたが、\(e^{\theta i}\) には指数法則が成り立ちます。 つまり、
\(\displaystyle e^{\theta i}e^{\phi i} = e^{(\theta+\phi)i}, \ \ \frac{e^{\theta i}}{e^{\phi i}} = e^{(\theta-\phi)i} \)となることが証明できます。 なお、これは、見た目には指数法則ですが、実際には例えば前者は、
\(\displaystyle (\cos\theta+i\sin\theta)(\cos\phi+i\sin\phi) =\cos(\theta+\phi)+i\sin(\theta+\phi) \)を意味し、簡単にそれが成り立つとは気がつきません。 実際には加法定理によってそれが成り立つことが示されます。
これにより、\(\cos\theta+i\sin\theta\) の形の式の積は 同じ形で角が和になること、 および \(\cos\theta+i\sin\theta\) の形の式の商は、 同じ形で角が差になることとなり、 そこから \(\cos\theta+i\sin\theta\) の形の式は、 指数的なもの、すなわち \(A^\theta\) のような形であることが予想されます。 ただし、これだけだと、それが \(e^{\theta i}\) の形になるところまでは いきません。
通常オイラーの公式の状況証拠としてよく用いられるのは 「マクローリン展開」による説明でしょう。 \(\cos x\) と \(\sin x\), \(e^x\) のマクローリン展開は、
\(\displaystyle \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \)のようになることが良く知られています。 上の 2 つを組み合わせると、なんとなく \(e^x\) がでてきそうな気がしますが、足しても引いても、 また \(-x\) を代入してもうまくいきません。 ところが \(e^x\) の右辺の \(x\) を \(xi\) に変えてみると、 すなわちマクローリン展開の式に「形式的に」実数 \(x\) の部分を 純虚数 \(xi\) に変えてみると、 \((xi)^2 = -x^2\), \((xi)^3 = -x^3i\), \((xi)^4 = x^4\) 等となるので、
\(\displaystyle \sin x = \frac{x}{1!} - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \)
\(\displaystyle e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots \)
\(\displaystyle e^{xi} = 1 + \frac{x}{1!}i - \frac{x^2}{2!} - \frac{x^3}{3!}i + \frac{x^4}{4!} + \cdots \)となり、これを実数部分と虚数部分に分けると、 それぞれが \(\cos x\)、\(\sin x\) のマクローリン展開の式になり、
\(\displaystyle e^{xi} = \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots\right) +\left(\frac{x}{1!} - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots\right)i = \cos x + i\sin x \)となってオイラーの公式が得られる、という仕組みです。 虚数乗 \(e^{xi}\) とはなんだろう、と考えた場合は、 こういう方向で式を作るのもある程度自然な気がします。
\(e\) の定義は、元々
\(\displaystyle e = \lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^n \)という数列の極限であることは良く知られています。さらに、ここから、 任意の実数 \(x\) に対して
\(\displaystyle \lim_{n\rightarrow\infty}\left(1+\frac{x}{n}\right)^n = e^x \)となることを示すこともできます。 実はオイラーの時代は、指数が負の整数や有理数乗まで 拡張はされていたものの、 まだ「実数乗」というものが厳密に定義されていたわけではなく、 だからむしろ良く知られていた対数関数から その逆関数として実数乗である指数関数を定義していたくらいです。
そんな中、オイラーは上の極限によって \(e\) の実数乗が定義できることに気がつきました。 すなわち、\(x\) が負の整数の場合も有理数の場合も その「数列の極限」による値と一致するので、 逆に \(x\) が無理数の場合もこれを使って無理数乗 (すなわちすべての実数乗) をこれで定義しよう、という方法です。
これは、現在教科書で広く行われている「有理数乗の極限」 として定義する方法よりもかなりシンプルな方法で、 指数としては整数乗、極限としては数列の極限しか使っていません。 もちろん、一般の \(a^x\) の定義を行う場合はそれだけでは足りずに、 自然対数 (のようなもの) が必要になります。
ところで、この極限で、\(x\) の代わりに \(xi\) とすると、すなわち
\(\displaystyle \lim_{n\rightarrow\infty}\left(1+\frac{xi}{n}\right)^n \)という複素数数列の極限を考えると、 実はそれが \(\cos x+i\sin x\) という複素数になることが証明できます (詳しくは「 指数関数の定義について」参照)。 よってここまでの流れを考えれば、 そこから \(e^{x i} = \cos x + i\sin x\) とみなす、 と考えるのも自然なことでしょう。
講義では、オイラーの公式 \(\displaystyle e^{\theta i}=\cos\theta+i\sin\theta\) に対して、指数法則
\(\displaystyle e^{\theta i}e^{\phi i} = e^{(\theta+\phi)i},\) \(\displaystyle \frac{e^{\theta i}}{e^{\phi i}} = e^{(\theta-\phi)i}\)が成り立つことを紹介し、前者は加法定理によって成り立つことを示しましたが、 後者の証明は省略しました。ここでその証明を紹介しておきます。
これは、前者の積の法則から出てきます。 つまり前者の式で、\(\theta\) の部分を \(\theta-\phi\) に変えると、
\(\displaystyle e^{(\theta-\phi)i}e^{\phi i} = e^{(\theta-\phi+\phi)i} = e^{\theta i}\)となるので、あとはこの両辺を \(e^{\phi i}\) で割ればいいだけです。 なお、\(|e^{\phi i}|=1\) なので \(e^{\phi i}\) が 0 になることはなく、それで割ることは常に可能です。 (01/17 2023)
講義で「一般二項展開」という \((1+x)^\alpha\) のマクローリン展開の式を簡単に紹介しましたが、これを用いると、 \(x^\alpha\) のテイラー展開などを微分を行わずに計算できます。 それをまとめてみたので、ここに置きます。
ただし、試験などで 「テイラー展開を求めよ」や「マクローリン展開を求めよ」という問題が出されたら、 それらの公式を正しく覚えていて使えるか、 ということを聞かれているのでしょうから、 本稿のような計算ではなく、定義通りに高階微分の計算をして求めるべきでしょう。 そうでないと減点される可能性があります。
積分の応用として、\(y=f(x)\) のグラフの [a,b] での曲線長 L を 求める公式
\(\displaystyle L = \int_a^b\sqrt{1+(f'(x))^2}\,dx\)を講義で紹介しましたが、 これを使って、いくつか簡単な関数の曲線長を計算してみたものを 以下に置きます。
