

Next: 4 最後に
Up: 3 次元のアフィン行列を求める問題について
Previous: 2 アフィン変換と回転行列
(PDF ファイル: system2.pdf)
私が聞いた、合同アフィン変換 (1) を決定する方法は
以下のような方法であった。
- 空間内の 3 点
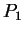 ,
, 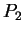 ,
, 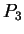 を、それらが三角形を作るように取る
(一直線上には取らない)
を、それらが三角形を作るように取る
(一直線上には取らない)
- それらのアフィン変換 (1) による像
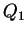 ,
, 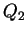 ,
, 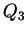 を
決め、そのようなアフィン変換を求める (具体的には回転行列
を
決め、そのようなアフィン変換を求める (具体的には回転行列 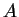 とベクトル
とベクトル
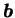 の成分を求める) ことを考える
の成分を求める) ことを考える
- 以下のようにベクトル
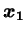 ,
,
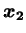 ,
,
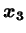 と
と
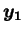 ,
,
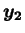 ,
,
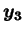 を決める
を決める
- すると、
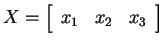 ,
,
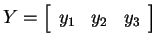 に対して
に対して
が成り立つので、両辺 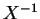 をかけて
をかけて 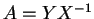 により
により 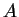 が求まり、
が求まり、
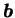 は式 (1) より
は式 (1) より
により求まる
方法は以上の通りであるが、しかしこれらの操作は
必ずしも自明ではない部分を含んでいる。
例えば
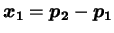 ,
,
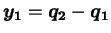 より、
より、
となり、同様にして
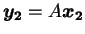 が成り立つことも分かるので
が成り立つことも分かるので
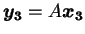 が成り立てば確かに
が成り立てば確かに 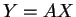 、すなわち
、すなわち
となるが、この
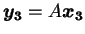 、すなわち
、すなわち
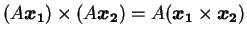 は明らかではないし、例えば一般の行列
は明らかではないし、例えば一般の行列 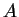 に対して成り立つ式ではない。
に対して成り立つ式ではない。
しかし、これは 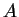 が回転行列の場合は成立する。
が回転行列の場合は成立する。
定理 1
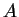 が直交行列で、
が直交行列で、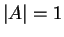 の場合、
の場合、
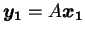 ,
,
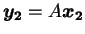 に対して
に対して
が成立する。
証明
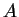 が直交行列、すなわち
が直交行列、すなわち 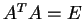 である場合、
である場合、
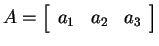 の
の
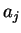 は互いに直交する単位ベクトルとなる。
また、
は互いに直交する単位ベクトルとなる。
また、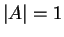 より
より
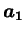 ,
,
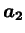 ,
,
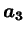 はこの順に右手系となる。よって、以下が成り立つ。
はこの順に右手系となる。よって、以下が成り立つ。
となる。
今、
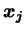 の各成分を
の各成分を
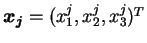
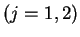 と書くことにすると、
と書くことにすると、
となるので、
となる。
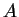 が求まれば、そこから平行移動成分
が求まれば、そこから平行移動成分
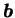 を求めるのは易しい。
を求めるのは易しい。


Next: 4 最後に
Up: 3 次元のアフィン行列を求める問題について
Previous: 2 アフィン変換と回転行列
Shigeharu TAKENO
2004年 2月 26日
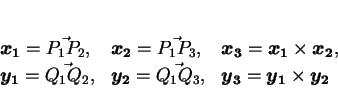
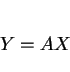
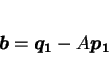
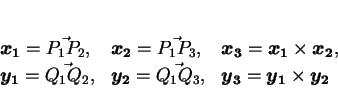
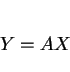
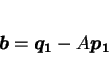
![]() ,
,
![]() より、
より、
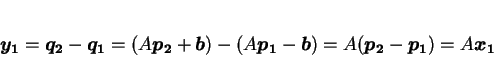
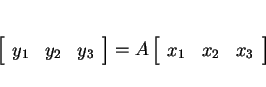
![]() が回転行列の場合は成立する。
が回転行列の場合は成立する。
![]() が直交行列で、
が直交行列で、![]() の場合、
の場合、
![]() ,
,
![]() に対して
に対して
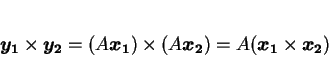
![]() が直交行列、すなわち
が直交行列、すなわち ![]() である場合、
である場合、
![]() の
の
![]() は互いに直交する単位ベクトルとなる。
また、
は互いに直交する単位ベクトルとなる。
また、![]() より
より
![]() ,
,
![]() ,
,
![]() はこの順に右手系となる。よって、以下が成り立つ。
はこの順に右手系となる。よって、以下が成り立つ。
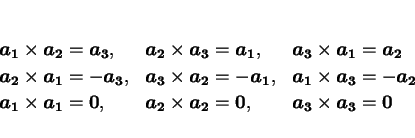
![]() の各成分を
の各成分を
![]()
![]() と書くことにすると、
と書くことにすると、
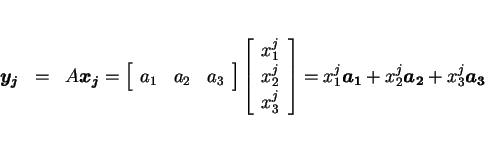
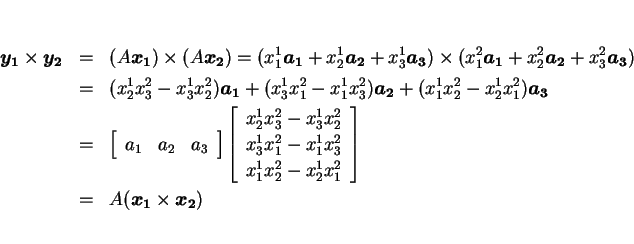
![]() が求まれば、そこから平行移動成分
が求まれば、そこから平行移動成分
![]() を求めるのは易しい。
を求めるのは易しい。