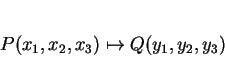
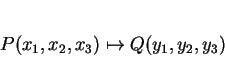
この変換によって、座標軸方向の単位ベクトル
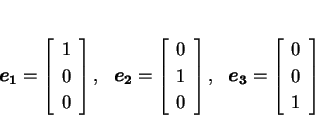
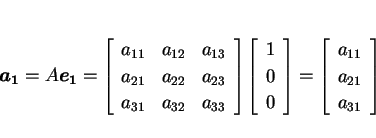
ここで、
![]() (内積) に等しいことを
利用して、この行列
(内積) に等しいことを
利用して、この行列 ![]() に関して
に関して ![]() (
(![]() は
は ![]() の転置) を計算してみると、
の転置) を計算してみると、
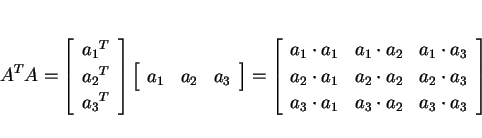
このように、![]() 、すなわち転置行列が逆行列となるような実行列は、
直交行列 と呼ばれているが、逆に、直交行列の列ベクトルは
上の計算からもわかるように互いに直交する単位ベクトルとなっている。
すなわち、合同変換を表す行列
、すなわち転置行列が逆行列となるような実行列は、
直交行列 と呼ばれているが、逆に、直交行列の列ベクトルは
上の計算からもわかるように互いに直交する単位ベクトルとなっている。
すなわち、合同変換を表す行列 ![]() は直交行列であることがわかる。
は直交行列であることがわかる。
また、直交行列は
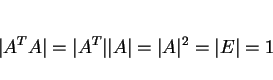
回転を表す行列は、さらに各軸の周りの回転角を用いて、3 つのパラメータ (角度) の正弦、余弦の値を使って表されるようであり、 詳しくは知らないのでここではそれは省略するが、 回転を表す行列が与えられれば、それらの角は一意に決定することができるようである。
また、![]() による変換が本当に原点の周りの回転を表しているのか、
ということに関しては、
一次変換の性質を次のように見れば多少納得できるだろう。
3 次元空間の任意の点
による変換が本当に原点の周りの回転を表しているのか、
ということに関しては、
一次変換の性質を次のように見れば多少納得できるだろう。
3 次元空間の任意の点
![]() が、
が、![]() によって
によって
![]() に写ったとすると、それらは
に写ったとすると、それらは
![]() の
関係にあるが、ここで、
の
関係にあるが、ここで、
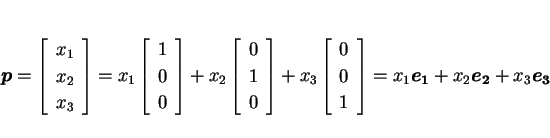
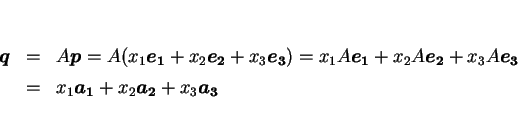
この式は、
![]() ,
,
![]() ,
,
![]() をあらたな座標軸として
点
をあらたな座標軸として
点 ![]() を見ると、その成分は
を見ると、その成分は ![]() ,
, ![]() ,
, ![]() であり、
それは、元の座標系での点
であり、
それは、元の座標系での点 ![]() の成分に等しい、
ということを意味している。
つまり、
の成分に等しい、
ということを意味している。
つまり、![]() による変換は、
座標軸が
による変換は、
座標軸が
![]() ,
,
![]() ,
,
![]() に合わせて方向を変えた分だけ
に合わせて方向を変えた分だけ
![]() も動く、そういう変換である、ということを意味することになる。
も動く、そういう変換である、ということを意味することになる。