 は常に
の形に書き表すことができる。
は常に
の形に書き表すことができる。
 は常に
の形に書き表すことができる。
は常に
の形に書き表すことができる。
この (7) は、単位球面の 3 次元極座標表現 (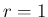 ) な
ので、明らかであるが、一応示しておく。
) な
ので、明らかであるが、一応示しておく。
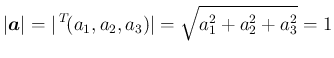
 、よって、
、よって、
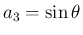 となる
となる 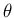 が
が
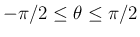 の範囲でただ一つ決定する。
の範囲でただ一つ決定する。
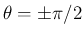 の場合は
の場合は 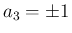 より、
より、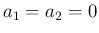 となり、
となり、
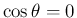 となるから
となるから 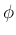 は例えば
は例えば 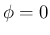 とでもすれば
よい (この場合
とでもすれば
よい (この場合 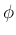 は一意には決まらない)。
は一意には決まらない)。
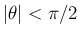 の場合は、
の場合は、
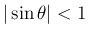 より
より
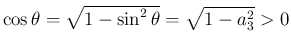 で、
で、
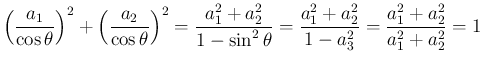
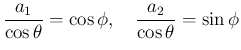
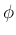 が
が
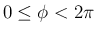 の範囲でただ一つ決定する。
の範囲でただ一つ決定する。
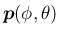 は、図 3 のように、
原点から単位球面へ向かうベクトルで、緯度 (中心からの仰角) が
は、図 3 のように、
原点から単位球面へ向かうベクトルで、緯度 (中心からの仰角) が 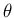 、
経度 (
、
経度 (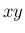 平面への射影の
平面への射影の 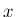 軸からの偏角) が
軸からの偏角) が 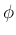 で
あるようなベクトルとなる。
で
あるようなベクトルとなる。
 ,
,
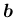 ,
,
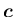 に対して、
行列式とスカラー三重積の値は等しい。
また、
に対して、
行列式とスカラー三重積の値は等しい。
また、
 ,
,
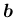 ,
,
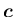 が作る平行六面体の体積を
が作る平行六面体の体積を 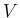 と
すると、
となる。
符号は、
と
すると、
となる。
符号は、
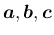 が右手系のときにプラス、
左手系のときにマイナスとなる。
が右手系のときにプラス、
左手系のときにマイナスとなる。
ベクトル解析の本を見れば大抵載っているが、一応示しておく。 (3) より、
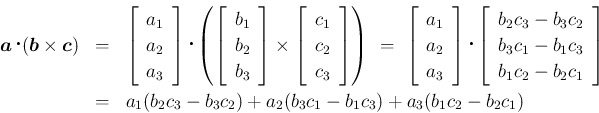
後半であるが、スカラー三重積はまず
であり、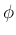 は
は
 と
と
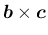 が
なす角 (
が
なす角 (
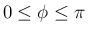 ) となる。
) となる。
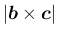 は、
は、
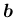 と
と
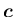 が作る
平行四辺形の面積になるので、それを平行六面体の底面と見れば、
その高さは、その底面に垂直な方向
が作る
平行四辺形の面積になるので、それを平行六面体の底面と見れば、
その高さは、その底面に垂直な方向
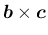 への、
への、
 の正射影
の正射影
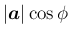 となる。
ただし、
となる。
ただし、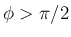 であれば
であれば 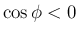 なので、
高さは
なので、
高さは
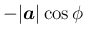 となる。
よって、(10) の右辺は
となる。
よって、(10) の右辺は 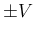 となる。
となる。
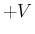 となるのは、
となるのは、
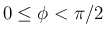 のときなので、
のときなので、
 が底面に対して
が底面に対して
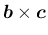 と同じ側にあるとき、
よって
と同じ側にあるとき、
よって
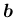 ,
,
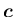 ,
,
 は右手系となるから、
は右手系となるから、
 ,
,
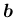 ,
,
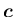 は右手系。
逆に
は右手系。
逆に 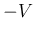 となるのは、
となるのは、
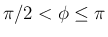 のときなので、
のときなので、
 が底面に対して
が底面に対して
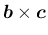 と反対側にある。
よって
と反対側にある。
よって
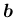 ,
,
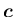 ,
,
 は左手系なので、
は左手系なので、
 ,
,
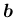 ,
,
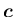 は左手系となる。
は左手系となる。
なお、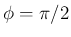 の場合は
の場合は 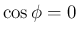 より三重積は 0 となるが、
この場合
より三重積は 0 となるが、
この場合
 ,
,
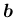 ,
,
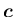 は同一平面にあるので
は同一平面にあるので 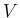 も 0 となり、やはり (9) は成立する。
も 0 となり、やはり (9) は成立する。
行列式の性質により、
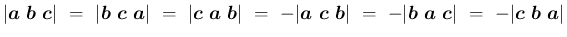
3 次元ベクトル
 ,
,
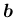 ,
,
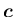 がいずれも
単位ベクトルで、互いに垂直な場合、これらを 正規直交系 と呼ぶ。
がいずれも
単位ベクトルで、互いに垂直な場合、これらを 正規直交系 と呼ぶ。
 ,
,
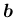 ,
,
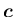 が正規直交系ならば
が正規直交系ならば
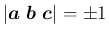 となることがわかる。
となることがわかる。
 ,
,
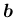 ,
,
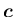 が右手系の正規直交系ならば
の形に表すことができる。
ここで、
が右手系の正規直交系ならば
の形に表すことができる。
ここで、
 は (7) の
右辺のベクトル、
は (7) の
右辺のベクトル、
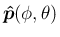 ,
,
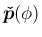 は、
は、
まず、
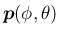 ,
,
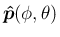 ,
,
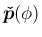 は正規直交系で、
は正規直交系で、
まず、
 を
を
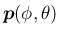 の形に書くことは、
補題 1 により可能で、
これに対し、
の形に書くことは、
補題 1 により可能で、
これに対し、
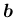 ,
,
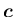 は
は
 に
垂直な平面上にあるので、
に
垂直な平面上にあるので、
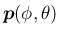 に垂直な単位ベクトル
に垂直な単位ベクトル
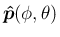 ,
,
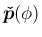 の
線形結合 (スカラー倍の和) で書けることになる。
しかも、
の
線形結合 (スカラー倍の和) で書けることになる。
しかも、
 ,
,
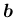 ,
,
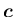 は右手系の正規直交系、
は右手系の正規直交系、
 ,
,
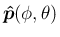 ,
,
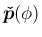 も
右手系の正規直交系なので、その平面上で、
も
右手系の正規直交系なので、その平面上で、
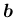 ,
,
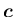 は、
は、
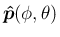 ,
,
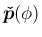 をある角だけ
をある角だけ
 を軸として回転したベクトルとなる (図 4)。
その角を
を軸として回転したベクトルとなる (図 4)。
その角を 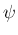 とすれば、
とすれば、
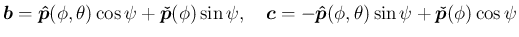
なお、参考までにこの (12) の成分をすべて書き下すと、
以下のようになる。
![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png) の列ベクトル
の列ベクトル
 ,
,
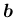 ,
,
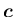 は正規直交系となる。
よって、
は正規直交系となる。
よって、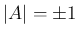 である。
である。
逆に、
 ,
,
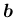 ,
,
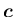 が正規直交系であれば、
が正規直交系であれば、
![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png) は直交行列となる。
は直交行列となる。
ベクトルはすべて列ベクトルなので、ベクトルの内積は、
転置行列との積で書けることに注意する。
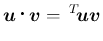
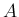 は直交行列であるから
は直交行列であるから
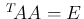 であるが、これは、
であるが、これは、
![$\displaystyle \,{}^T\!{A}A
=
\left[\begin{array}{c}{\,{}^T\!{\mbox{\boldmath...
...egin{array}{ccc}{1}&{0}&{0}\\
{0}&{1}&{0}\\
{0}&{0}&{1}\end{array}\right]
$](img103.png)
 ,
,
 ,
,
 は正規直交系となる。
は正規直交系となる。
逆に、
 ,
,
 ,
,
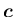 は正規直交系であれば、
上の計算より
は正規直交系であれば、
上の計算より
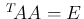 となることがわかる。
行列式の理論により、
となることがわかる。
行列式の理論により、
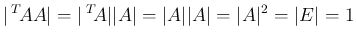
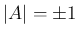 となるから、
となるから、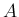 は逆行列
は逆行列 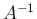 を持ち、
よって
を持ち、
よって
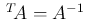 となり、
となり、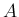 は直交行列となる。
は直交行列となる。
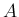 に対し、
に対し、
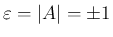 とすると、
任意のベクトル
とすると、
任意のベクトル
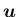 ,
,
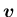 に対し、
に対し、
![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png) 、
とすると、補題 4 より
、
とすると、補題 4 より
 ,
,
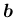 ,
,
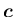 は正規直交系で、
は正規直交系で、
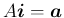 ,
,
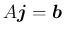 ,
,
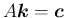 であり、
補題 2 より、
であり、
補題 2 より、
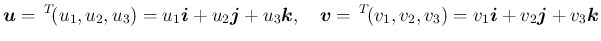
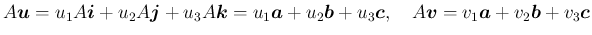
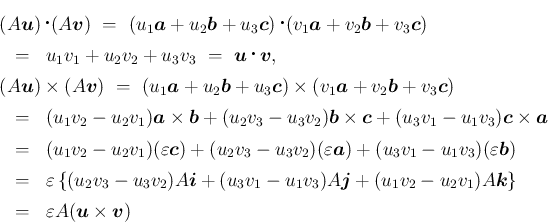
なお、(18) の内積の方は、行列の積を用いて
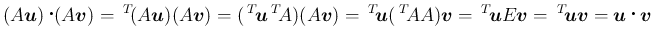
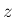 軸を回転軸とする
軸を回転軸とする 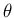 回転 (回転軸ベクトル
回転 (回転軸ベクトル
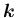 ) は、
図 4 と同様に考えれば、
) は、
図 4 と同様に考えれば、
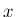 軸方向の単位ベクトル
軸方向の単位ベクトル
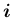 を
を
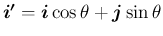 に、
に、
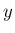 軸方向の単位ベクトル
軸方向の単位ベクトル
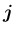 を
を
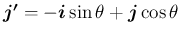 に移動することがわかる。
そしてそれにともない、点 P
に移動することがわかる。
そしてそれにともない、点 P の位置ベクトル
の位置ベクトル
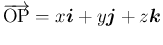 は、
は、
![$\displaystyle \overrightarrow{\mathrm{OP'}}=x\mbox{\boldmath$i'$}+y\mbox{\boldm...
...\cos\theta}&{0}\\
{0}&{0}&{1}\end{array}\right]
\overrightarrow{\mathrm{OP}}
$](img122.png)
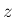 軸に関する
軸に関する 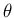 回転は、行列
による一次変換で表されることになる。
この
回転は、行列
による一次変換で表されることになる。
この 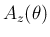 を
を 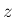 軸に関する 軸回転行列 と呼ぶ。
軸に関する 軸回転行列 と呼ぶ。
同様に、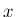 軸の
軸の 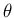 回転は、
回転は、
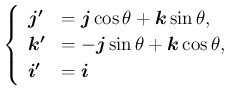
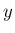 軸の
軸の 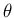 回転は、
回転は、
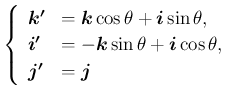
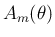
 , および任意の角
, および任意の角 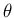 ,
, 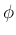 に
対して、次が成り立つ。
に
対して、次が成り立つ。
例えば 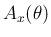 で考えれば、
で考えれば、
![\begin{eqnarray*}\lefteqn{A_x(\theta)A_x(\phi)
\ =\
\left[\begin{array}{ccc}{...
...&{\cos(\theta+\phi)}\end{array}\right]
\ =\
A_x(\theta+\phi)
\end{eqnarray*}](img133.png)
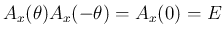 となるから、
後半もすぐに得られる。
となるから、
後半もすぐに得られる。
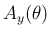 ,
, 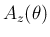 の場合も同様。
の場合も同様。
一般的ではないが、本稿では次のような記号も用いる。
3 次正方行列
![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png) と
3 次元列ベクトル
と
3 次元列ベクトル
 に対して、
に対して、
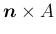 は 3 次の正方行列となる。
は 3 次の正方行列となる。
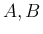 , および 3 次元列ベクトル
, および 3 次元列ベクトル
 ,
,
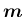 に対して、次が成り立つ。
に対して、次が成り立つ。
(25) の前者が成り立つとすると、
後者が示されることを先に示す。
![$B=[\mbox{\boldmath$b$}_1,\mbox{\boldmath$b$}_2,\mbox{\boldmath$b$}_3]$](img141.png) とすると、
とすると、
![$AB = [A\mbox{\boldmath$b$}_1,A\mbox{\boldmath$b$}_2,A\mbox{\boldmath$b$}_3]$](img142.png) より
より
![$\displaystyle \mbox{\boldmath$n$}\times (AB)
= \mbox{\boldmath$n$}\times[A\mb...
...(A\mbox{\boldmath$b$}_2),
\mbox{\boldmath$n$}\times(A\mbox{\boldmath$b$}_3)]
$](img143.png)
![$\displaystyle [(\mbox{\boldmath$n$}\times A)\mbox{\boldmath$b$}_1,
(\mbox{\bol...
...\mbox{\boldmath$b$}_2,\mbox{\boldmath$b$}_3]
=(\mbox{\boldmath$n$}\times A)B
$](img144.png)
よってあとは (25) の前者を示せばよい。
![$A=[\mbox{\boldmath$a$}_1,\mbox{\boldmath$a$}_2,\mbox{\boldmath$a$}_3]$](img145.png) ,
,
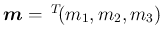 とすると、
とすると、
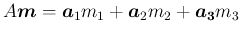 なので、
なので、
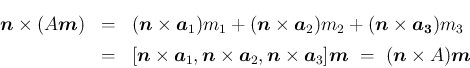
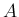 の固有値
の固有値 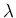 はすべて
はすべて 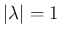 。
特に、3 次の直交行列では、必ず
。
特に、3 次の直交行列では、必ず 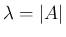 という固有値を持つ。
という固有値を持つ。
複素数ベクトル
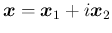 ,
,
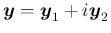 (
(
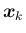 ,
,
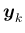 は
実数ベクトル、
は
実数ベクトル、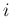 は虚数単位) の内積
は虚数単位) の内積
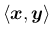 、
大きさ
、
大きさ
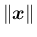 を、
を、
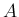 の固有値を
の固有値を 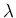 、それに対する固有ベクトルを
、それに対する固有ベクトルを
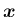 とする。
とする。
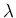 は一般には複素数
は一般には複素数
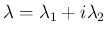 、
、
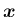 は複素数ベクトル
は複素数ベクトル
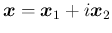 で、
ゼロベクトルではない。
で、
ゼロベクトルではない。
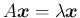 なので、
なので、
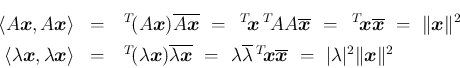
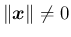 より
より 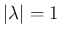 が得られる。
が得られる。
よって実数の固有値は 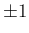 のいずれかとなるが、
3 次の直交行列の固有方程式
のいずれかとなるが、
3 次の直交行列の固有方程式
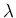 はすべて
はすべて 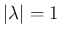 なので、
なので、
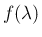 は以下のいずれかの形となる。
は以下のいずれかの形となる。
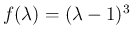
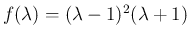
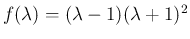
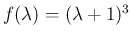
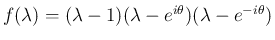
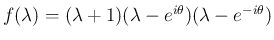
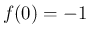
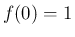
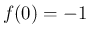
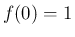
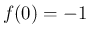
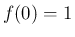
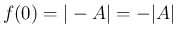 でなければいけないので、
でなければいけないので、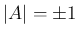 より、
より、
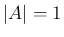 のときは定数項は
のときは定数項は 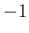 だから上の 1. か 3. か 5. で、
この場合はいずれも
だから上の 1. か 3. か 5. で、
この場合はいずれも 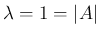 を解に持つ。
を解に持つ。
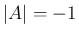 のときは定数項は
のときは定数項は 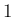 だから上の 2. か 4. か 6. で、
この場合もいずれも
だから上の 2. か 4. か 6. で、
この場合もいずれも
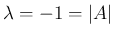 を解に持つ。
を解に持つ。
なお、3 次の直交行列の場合は、
固有方程式の具体的な因数分解もそれほど難しくない。
![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png) とすると、
とすると、
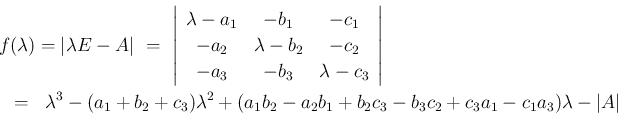
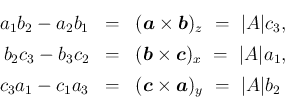
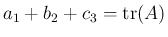 と書けば、
と書けば、
 ,
,
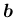 ,
,
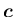 は単位ベクトルなので、
は単位ベクトルなので、
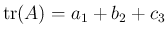 は、
は、
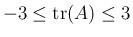 となるが、
その範囲はもう少し狭くなる。
となるが、
その範囲はもう少し狭くなる。
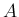 の対角成分の和
の対角成分の和
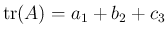 は、
は、
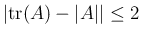
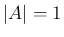 なら
なら
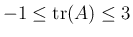 ,
,
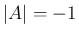 なら
なら
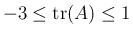 である。
である。
(29) より、右側の 2 次方程式
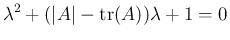
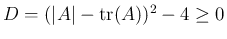 の場合、
補題 8 よりその解はすべて
の場合、
補題 8 よりその解はすべて 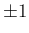 でなくてはならない。
よって、
でなくてはならない。
よって、
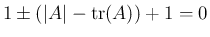 より
より
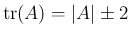 となり
この場合は補題が成立する。
となり
この場合は補題が成立する。
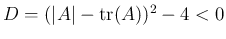 の場合は、
の場合は、
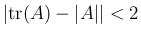 と
なるのでやはり補題は成立する。
なお、この
と
なるのでやはり補題は成立する。
なお、この 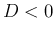 の場合は、解は
の場合は、解は
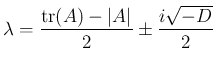
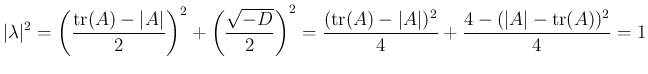
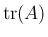 の最大値、最小値を考えるには、
の最大値、最小値を考えるには、
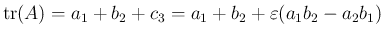 と
書くこともできるので、
と
書くこともできるので、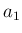 ,
, 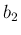 ,
, 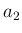 ,
, 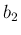 を変数と見て
考えることもできるが、
制約条件が色々あるため、その方向ではかなり難しい。
を変数と見て
考えることもできるが、
制約条件が色々あるため、その方向ではかなり難しい。
竹野茂治@新潟工科大学