![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png)
![$A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]$](img99.png) による
一次変換が、
による
一次変換が、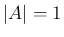 の場合は 3 節で述べた回転変換となり、
の場合は 3 節で述べた回転変換となり、
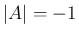 の場合は回転変換と反転の合成となることを示す。
そして、回転軸ベクトル
の場合は回転変換と反転の合成となることを示す。
そして、回転軸ベクトル
 と回転角
と回転角  の具体的な
計算方法についても考察する。
の具体的な
計算方法についても考察する。
まず、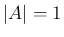 の場合を考える。
補題 8 より、
の場合を考える。
補題 8 より、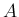 は固有値 1 を持ち、
その単位固有ベクトル (実数ベクトル) のひとつを
は固有値 1 を持ち、
その単位固有ベクトル (実数ベクトル) のひとつを
 とする。
とする。
 を
を
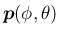 の形で表すことができる。ここで、
の形で表すことができる。ここで、
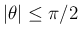 ,
,
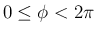 であるが、
であるが、
 の場合は、
の場合は、
 の代わりに
の代わりに
 と
取り直すことによって、
と
取り直すことによって、 とできるので、
とできるので、
 としてよい。
また、
としてよい。
また、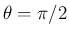 のとき (
のとき (
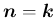 ) は、
) は、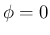 とする。
とする。
補題 3 より、
 ,
,
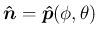 ,
,
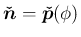 は
右手系の正規直交系となる。
は
右手系の正規直交系となる。
 ,
,
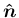 ,
,
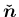 の
の 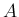 による像
による像
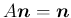 ,
,
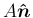 ,
,
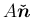 は、
補題 5 により
やはり互いに直交する単位ベクトルとなり、
は、
補題 5 により
やはり互いに直交する単位ベクトルとなり、
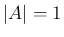 より
より
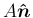 ,
,
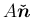 は、
は、
 に垂直な面上で
に垂直な面上で
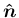 ,
,
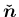 を
回転したものになるので (図 4 と同様)、
その回転角を
を
回転したものになるので (図 4 と同様)、
その回転角を 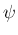 とすれば、
と書けることになる。
すなわち、任意の 3 次元ベクトル
とすれば、
と書けることになる。
すなわち、任意の 3 次元ベクトル
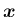 を
正規直交系
を
正規直交系
 ,
,
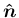 ,
,
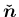 を用いて
を用いて
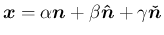
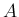 による像は、
による像は、
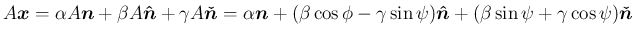
 方向の成分は不変で、
方向の成分は不変で、
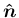 ,
,
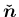 に関する回転となっていることがわかる。
これにより、
に関する回転となっていることがわかる。
これにより、 が
が
 を回転軸ベクトルとする
を回転軸ベクトルとする  回転を
表すことが示された。
回転を
表すことが示された。
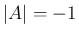 の場合は、固有値は
の場合は、固有値は 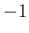 で、(30) が
で、(30) が
 ,
,
 ,
,
 の像
の像
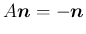 ,
,
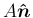 ,
,
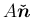 は、
左手系の正規直交系となる。
は、
左手系の正規直交系となる。
 方向の反転変換を
方向の反転変換を 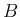 とすると、
とすると、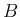 は、
は、
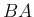 を考えれば、
を考えれば、
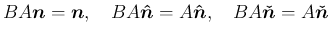
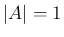 の場合と同様にして、
の場合と同様にして、
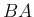 は回転軸ベクトル
は回転軸ベクトル
 に関する
に関する 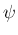 の回転変換となる。
すなわち、
の回転変換となる。
すなわち、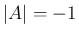 の場合は、
の場合は、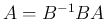 は、回転変換
は、回転変換 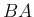 と、
と、
 方向の反転変換
方向の反転変換 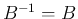 の合成変換であることがわかる。
の合成変換であることがわかる。
これで本節の目的の前半部分が示されたことになる。
次は、具体的な回転軸ベクトルと回転角の計算方法について考える。
回転軸ベクトル
 は、既に述べたように固有値
は、既に述べたように固有値 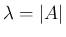 に
対する単位固有ベクトルを取ればよいので
に
対する単位固有ベクトルを取ればよいので 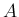 から回転軸ベクトルを計算することは難しくない。
から回転軸ベクトルを計算することは難しくない。
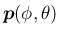 の
の 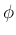 ,
, 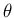 を確定する代わりに、
を確定する代わりに、
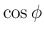 ,
, 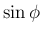 等を求めることを考える。
等を求めることを考える。
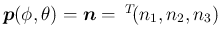 で、
上に述べたように
で、
上に述べたように 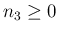 としてよいから、
としてよいから、
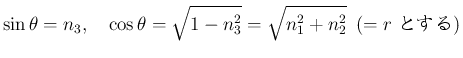
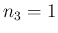 ならば
ならば 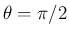 ,
, 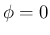 より
より 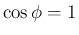 ,
,  で、
で、
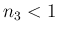 ならば
ならば
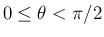 ,
, 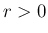 で、
で、
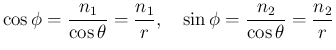
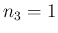 ならば
ならば
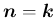 ,
,
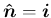 ,
,
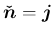 、
、
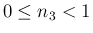 ならば
ならば
![$\displaystyle \mbox{\boldmath$\hat{n}$}
=\left[\begin{array}{c}{\cos\phi\sin\th...
...rray}\right]
=\left[\begin{array}{c}{-n_2/r}\\ {n_1/r}\\ {0}\end{array}\right]
$](img251.png)
 の成分を使って表すことができるから、
間接的に
の成分を使って表すことができるから、
間接的に 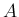 の成分で表せることになる。
の成分で表せることになる。
回転角 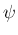 については、
については、
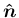 、
、
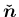 の像
(32) の右辺は、
丁度 (16), (17) の式に一致するので、
その
の像
(32) の右辺は、
丁度 (16), (17) の式に一致するので、
その 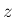 成分から計算できることがわかる。
すなわち、
成分から計算できることがわかる。
すなわち、
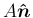 の
の 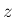 成分を
成分を 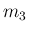 、
、
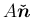 の
の 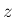 成分を
成分を 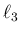 とすると、
これらは
とすると、
これらは
 と
と 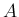 の成分で表すことができ、
の成分で表すことができ、
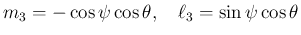
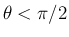 のときは
のときは
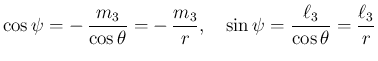
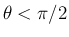 のときは回転角
のときは回転角 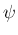 が一意に決定する。
が一意に決定する。
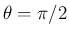 の場合は
の場合は 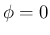 より
より
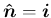 ,
,
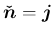 で、
で、
![$\displaystyle A\mbox{\boldmath$\hat{n}$}=\left[\begin{array}{c}{\cos\psi}\\ {\sin\psi}\\ {0}\end{array}\right]
$](img257.png)
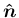 の
の 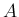 による像の
による像の 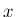 成分
成分 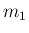 ,
, 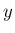 成分
成分 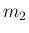 から
から 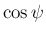 ,
, 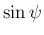 が計算できることになる。
が計算できることになる。
なお、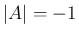 の場合の反転変換
の場合の反転変換  の行列表現であるが、
これは、(35) より、
の行列表現であるが、
これは、(35) より、
![$[\mbox{\boldmath$n$},\mbox{\boldmath$\hat{n}$},\mbox{\boldmath$\check{n}$}]$](img263.png) の
逆行列、すなわちその転置行列をかければ、
により得られる。
の
逆行列、すなわちその転置行列をかければ、
により得られる。
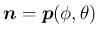 ,
,
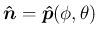 ,
,
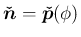 を使って
実際に計算してみる。
を使って
実際に計算してみる。
![\begin{eqnarray*}\lefteqn{B \ =\
[-\mbox{\boldmath$n$},\mbox{\boldmath$\hat{n}...
...ldmath$\alpha$},\mbox{\boldmath$\beta$},\mbox{\boldmath$\gamma$}]\end{eqnarray*}](img266.png)
![\begin{eqnarray*}\mbox{\boldmath$\alpha$}
&=&
\left[\begin{array}{c}{-\cos^2\p...
...ght]
\ (=\ \mbox{\boldmath$k$}-(2\sin\theta)\mbox{\boldmath$n$})\end{eqnarray*}](img267.png)
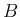 は対称行列となるので、
よって
は対称行列となるので、
よって
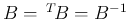 より、
より、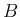 も直交行列となる。
さらによく見ると、
も直交行列となる。
さらによく見ると、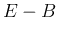 が少し易しい形になることがわかる。
が少し易しい形になることがわかる。
![$\displaystyle E-B
= [(2\cos\phi\cos\theta)\mbox{\boldmath$n$},
(2\sin\phi\cos\...
...theta)\mbox{\boldmath$n$}]
=
2\mbox{\boldmath$n$}\,{}^T\!{\mbox{\boldmath$n$}}
$](img270.png)
 から容易に計算できる。
なお、
から容易に計算できる。
なお、
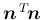 は
は 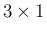 行列と
行列と 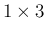 行列の積だから
行列の積だから 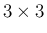 行列となっている
ことに注意する。
行列となっている
ことに注意する。
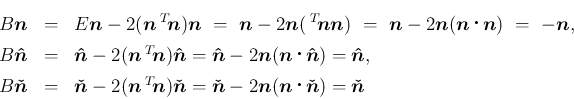
なお、(38) は別な方法でも導くことができる。
(37) より、
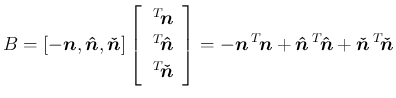
![$N=[\mbox{\boldmath$n$},\mbox{\boldmath$\hat{n}$},\mbox{\boldmath$\check{n}$}]$](img277.png) とすると、
これは直交行列となり、
とすると、
これは直交行列となり、
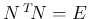 であるから、
となる。これにより、
であるから、
となる。これにより、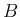 は、
は、
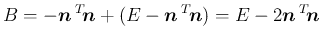
同様にして、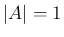 の直交行列
の直交行列 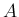 を、(32) を用いて
を、(32) を用いて
 で表すことを考えてみる。
(32) より、
で表すことを考えてみる。
(32) より、
![\begin{eqnarray*}AN
&=&
A[\mbox{\boldmath$n$},\mbox{\boldmath$\hat{n}$},\mbox...
...},\mbox{\boldmath$\check{n}$},-\mbox{\boldmath$\hat{n}$}]\sin\psi\end{eqnarray*}](img281.png)
![$[\mbox{\boldmath$0$},\mbox{\boldmath$\check{n}$},-\mbox{\boldmath$\hat{n}$}]
= ...
...x{\boldmath$n$}\times\mbox{\boldmath$\check{n}$}]
=\mbox{\boldmath$n$}\times N
$](img282.png) より
より

+N\cos\psi +(\mbox{\boldmath$n$}\times N)\sin\psi
$](img283.png)
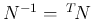 をかけると、
をかけると、
![$\displaystyle A
=
[\mbox{\boldmath$n$},\mbox{\boldmath$0$},\mbox{\boldmath$0$}]...
...os\psi)
+N\,{}^T\!{N}\cos\psi+(\mbox{\boldmath$n$}\times N)\,{}^T\!{N}\sin\psi
$](img285.png)
![$[\mbox{\boldmath$n$},\mbox{\boldmath$0$},\mbox{\boldmath$0$}]\,{}^T\!{N} = \mbox{\boldmath$n$}\,{}^T\!{\mbox{\boldmath$n$}}$](img286.png) ,
,
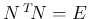 で、補題 7 より
で、補題 7 より
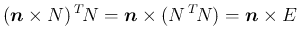
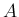 を回転軸ベクトル (1 の固有ベクトル)
を回転軸ベクトル (1 の固有ベクトル)
 と
回転角
と
回転角 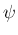 で表すことができたことになる。
で表すことができたことになる。
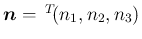 の成分で表せば、
の成分で表せば、
![\begin{eqnarray*}\mbox{\boldmath$n$}\,{}^T\!{\mbox{\boldmath$n$}}
&=& [n_in_j]...
...{n_2}\\
{n_3}&{0}&{-n_1}\\
{-n_2}&{n_1}&{0}\end{array}\right]\end{eqnarray*}](img290.png)
![$\displaystyle A
=
(\cos\psi)E
+(1-\cos\psi)\mbox{\boldmath$n$}\,{}^T\!{\mbox{\b...
...th$n$}\times E
=
[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]
$](img291.png)
竹野茂治@新潟工科大学