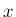 軸、
軸、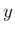 軸、
軸、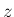 軸を
自然に表すことができるものを指し、そうでないものを左手系と呼ぶ (図 1)。
また、これらは必ずしも直交軸だけではなく、
同一平面上にない 3 つのベクトルに対しても同様の意味で用いられることもある。
軸を
自然に表すことができるものを指し、そうでないものを左手系と呼ぶ (図 1)。
また、これらは必ずしも直交軸だけではなく、
同一平面上にない 3 つのベクトルに対しても同様の意味で用いられることもある。
右手系とは、右手の親指、人差し指、中指でそれぞれ 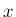 軸、
軸、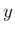 軸、
軸、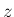 軸を
自然に表すことができるものを指し、そうでないものを左手系と呼ぶ (図 1)。
また、これらは必ずしも直交軸だけではなく、
同一平面上にない 3 つのベクトルに対しても同様の意味で用いられることもある。
軸を
自然に表すことができるものを指し、そうでないものを左手系と呼ぶ (図 1)。
また、これらは必ずしも直交軸だけではなく、
同一平面上にない 3 つのベクトルに対しても同様の意味で用いられることもある。
又は、指ではなく右ねじを使って
「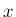 軸の正の方向を
軸の正の方向を 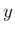 軸の正の方向に
軸の正の方向に 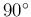 回転する向きに
右ねじを回したときに、ねじの進む方向が
回転する向きに
右ねじを回したときに、ねじの進む方向が 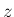 軸と一致する場合が
右手系」という表現もある (図 2)。
軸と一致する場合が
右手系」という表現もある (図 2)。
これらはいずれにせよ、視覚的な説明であり、数式による定義ではない。 では、数式で右手系か左手系かを定義することはできないのだろうか。
例えば、3 次元ベクトルの外積
は、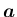 ,
,
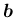 に垂直なベクトルで、
という性質が知られているので、それを利用すれば、
に垂直なベクトルで、
という性質が知られているので、それを利用すれば、
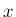 軸、
軸、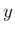 軸、
軸、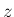 軸の正の方向の単位ベクトル
軸の正の方向の単位ベクトル
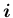 ,
,
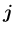 ,
,
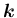 に対して
とすれば図を用いずに右手系を数式で定義できそうだが、
残念ながらこれはうまくいかない。
それは、
に対して
とすれば図を用いずに右手系を数式で定義できそうだが、
残念ながらこれはうまくいかない。
それは、
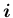 ,
,
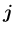 ,
,
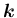 が右手系か左手系かに関わらず、
常に
が右手系か左手系かに関わらず、
常に
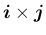 と
と
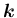 は同じ向きとなる (より詳しくは
は同じ向きとなる (より詳しくは
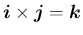 となる) からである。
となる) からである。
つまり、「
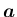 ,
,
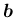 ,
,
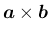 」は、
実は右手系になるのではなく、
常に軸方向
」は、
実は右手系になるのではなく、
常に軸方向
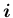 ,
,
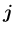 ,
,
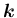 と同じ手系になり、
よって、座標軸が右手系なら
と同じ手系になり、
よって、座標軸が右手系なら
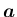 ,
,
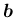 ,
,
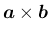 も右手系、座標軸が左手系なら左手系になる
だけなのである。
も右手系、座標軸が左手系なら左手系になる
だけなのである。
だから、(4) の性質を持つためには、 元々「座標系が右手系である」という前提が必要であり、 どの本でも、外積を定義する前 (あるいは少なくとも外積の基本性質を述べる前) に、 必ず「座標系は右手系と仮定する」という意味の文言が書かれているはずである。
逆に外積を図形的に定義して、そこから (3) を 導く順番で説明する本もあるが、 それもやはり座標系が右手系という仮定がなければ、 (3) を得ることはできない。
外積によって、任意のベクトルの組が、規準となる座標系と同じ手系か 異なる手系かの判断はできても、座標系の規準自体を決めるのに 外積を用いることはできない。
他にも、行列式
は、ベクトル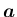 ,
,
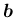 ,
,
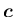 のスカラー三重積
のスカラー三重積
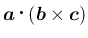 に一致し、
それは
に一致し、
それは
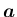 ,
,
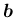 ,
,
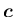 が作る平行六面体の
符号付き体積となり、その符号は、
が作る平行六面体の
符号付き体積となり、その符号は、
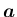 ,
,
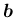 ,
,
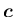 が右手系ならばプラス、
が右手系ならばプラス、
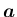 ,
,
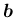 ,
,
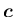 が左手系ならばマイナスとなる、
ということが知られている (4 節 補題 2) が、
これもあくまで座標軸が右手系である、という前提の話で、
座標軸が左手系ならば、手系と行列式の符号の関係は逆になる。
が左手系ならばマイナスとなる、
ということが知られている (4 節 補題 2) が、
これもあくまで座標軸が右手系である、という前提の話で、
座標軸が左手系ならば、手系と行列式の符号の関係は逆になる。
つまり、外積と同じで、座標軸の手系と同じか違うかは確認できても、
それを座標軸の手系を定義することには使えない。
実際、
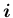 ,
,
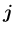 ,
,
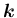 の手系に関わらず
の手系に関わらず
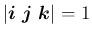 となってしまう。
となってしまう。
実は、数式で座標系の手系を規程することはできず、 例えば座標軸を「左手系」にしても、外積などで出てくる手系の話をすべて逆にすれば 「左手系のベクトル解析」は矛盾なく成立するのである。
本稿も、図 1 のような図による手系の定義により、 座標軸は右手系と取ることとしておく。
竹野茂治@新潟工科大学