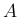 で、
で、
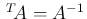 となるもの (本稿では
となるもの (本稿では 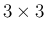 行列のみ)
行列のみ)
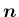 を 回転軸ベクトル と呼ぶ) に
対する角
を 回転軸ベクトル と呼ぶ) に
対する角 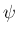 の回転をなす 3 次元空間の一次変換
の回転をなす 3 次元空間の一次変換
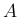 で、
で、
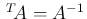 となるもの (本稿では
となるもの (本稿では 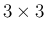 行列のみ)
行列のみ)
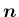 を 回転軸ベクトル と呼ぶ) に
対する角
を 回転軸ベクトル と呼ぶ) に
対する角 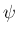 の回転をなす 3 次元空間の一次変換
の回転をなす 3 次元空間の一次変換
回転変換の回転方向は、その回転の向きに右ねじを回すとねじが進む方向が
回転軸ベクトル
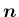 と一致するように考えることにする。
よって、回転軸ベクトル
と一致するように考えることにする。
よって、回転軸ベクトル
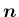 に関する角
に関する角 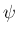 の回転と
回転軸ベクトル
の回転と
回転軸ベクトル
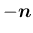 に関する角
に関する角 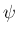 の回転は逆向きで、
の回転は逆向きで、
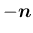 に関する
に関する 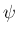 の回転は、
の回転は、
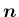 に関する
に関する 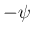 の回転と同じと考える。
の回転と同じと考える。
座標軸が右手系であれば、回転軸ベクトル
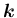 に対する
に対する 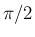 の回転は、
の回転は、
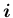 を
を
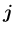 に一致させる回転に等しい。
に一致させる回転に等しい。
竹野茂治@新潟工科大学