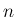
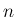 次元空間に関する一般論を教えるが、
逆に物理や工学などではより重要な 3 次元の 1 次変換の各論、
例えば回転変換などは普通は教えず、
「直交行列で行列式が 1 のものは回転を意味する」という話も、
それに触れることがあるかないか位だろうと思う。
次元空間に関する一般論を教えるが、
逆に物理や工学などではより重要な 3 次元の 1 次変換の各論、
例えば回転変換などは普通は教えず、
「直交行列で行列式が 1 のものは回転を意味する」という話も、
それに触れることがあるかないか位だろうと思う。
私自身もちゃんと把握はしていなかったので、 あらためて直交行列と回転変換について少し考察してみたことを ここにまとめておく。
なお、本稿では、ベクトルはすべて列ベクトル
のカンマ区切りの丸かっこの形で書くこととし、 横に成分を書くときは、行列の転置の記号を用いて の、行列とベクトルを混在したような記号で書くことにする。
また、行列も基本的に 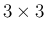 の行列のみを扱うが、
行列を列ベクトルを使って
の行列のみを扱うが、
行列を列ベクトルを使って
![$\displaystyle A=\left[\begin{array}{ccc}{a_1}&{b_1}&{c_1}\\
{a_2}&{b_2}&{c_2}...
...array}\right]
=[\mbox{\boldmath$a$}\ \mbox{\boldmath$b$}\ \mbox{\boldmath$c$}]
$](img10.png)
![$\displaystyle A=[\mbox{\boldmath$a$},\mbox{\boldmath$b$},\mbox{\boldmath$c$}]
$](img11.png)
竹野茂治@新潟工科大学