![$\displaystyle
Q^{-1}AQ
= J = \left[\begin{array}{ccc}J(\lambda_1,k_1) & \mult...
...lticolumn{2}{l}{\raisebox{0ex}{\LARGE$0$}} & J(\lambda_s,k_s)\end{array}\right]$](img197.png) (12)
(12)
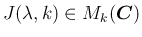 は、
対角成分が
は、
対角成分が 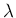 で、その一つ右上の斜め列に 1 が並ぶ
で、その一つ右上の斜め列に 1 が並ぶ 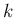 次の上三角行列
であり、ジョルダン細胞と呼ばれる。
次の上三角行列
であり、ジョルダン細胞と呼ばれる。
(12) の 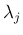 は
は 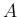 の固有値で、
各ジョルダン細胞
の固有値で、
各ジョルダン細胞
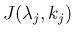 の
の 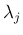 は
すべて異なるとは限らず、
は
すべて異なるとは限らず、
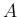 の固有値
の固有値 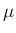 の重複度を
の重複度を 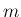 (固有方程式の
(固有方程式の 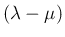 に関する因数が
に関する因数が
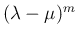 ) とすれば、
) とすれば、
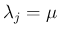 となるジョルダン細胞のサイズ
となるジョルダン細胞のサイズ 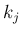 の和が
の和が 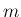 に
一致する。
に
一致する。
つまり、ジョルダン標準形 (12) の対角成分は
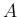 の固有値が重複度の分だけ並び、その一つ右上の斜め列には 0 か 1
が並んだ形となる。
の固有値が重複度の分だけ並び、その一つ右上の斜め列には 0 か 1
が並んだ形となる。
ジョルダン標準形を求めるには、まず 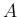 の固有値を求め、
その固有ベクトルを固有空間の次元分求める必要がある。
例えば、固有値
の固有値を求め、
その固有ベクトルを固有空間の次元分求める必要がある。
例えば、固有値 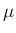 の重複度が
の重複度が 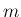 で、
固有空間の次元が
で、
固有空間の次元が 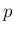 である場合は一般に
である場合は一般に 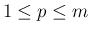 で、
で、
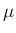 に対する一次独立な
に対する一次独立な 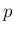 個の固有ベクトル
個の固有ベクトル
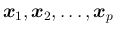 が得られる。
が得られる。
そして 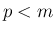 の場合は、各
の場合は、各
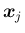 に対し、
広義固有ベクトルと呼ばれることもある
次のような
に対し、
広義固有ベクトルと呼ばれることもある
次のような
 でないベクトルの列
でないベクトルの列
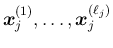 を求めていく。
を求めていく。
![\begin{eqnarray*}A[\mbox{\boldmath$x$}^{(1)}_{j}\ \mbox{\boldmath$x$}^{(2)}_{j}\...
...2)}_{j}\cdots\ \mbox{\boldmath$x$}^{(\ell_j)}_{j}]
J(\mu,\ell_j)\end{eqnarray*}](img216.png)
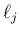 個の広義固有ベクトルが、
一つのジョルダン細胞
個の広義固有ベクトルが、
一つのジョルダン細胞 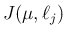 に対応することになる。
に対応することになる。
この作業をすべての
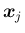 に対して行えば、
広義固有ベクトルの総数
に対して行えば、
広義固有ベクトルの総数
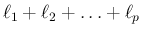 は
は 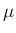 の
重複度
の
重複度 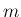 に一致することが知られていて、
よって固有値
に一致することが知られていて、
よって固有値 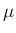 に対応するジョルダン細胞をすべて構成することが
できることになる。
に対応するジョルダン細胞をすべて構成することが
できることになる。
そしてここまでの作業をすべての固有値に対して行えば、
得られる広義固有ベクトルの総数は 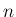 となり、
それらを順に列ベクトルとして並べた行列が
となり、
それらを順に列ベクトルとして並べた行列が 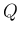 となって、
(12) が得られることになる。
となって、
(12) が得られることになる。
ジョルダン細胞に関する命題を 2,3 紹介する。
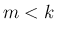 ならば
ならば 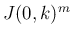 は
は 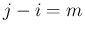 である
である 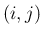 成分、
すなわち対角成分の右上
成分、
すなわち対角成分の右上 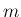 列目のななめ成分がすべて 1 で、
他はすべて 0 の行列、
列目のななめ成分がすべて 1 で、
他はすべて 0 の行列、
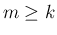 ならば
ならば 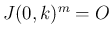 。
。
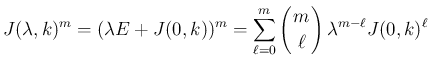
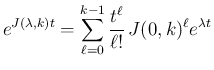
1., 2. は簡単な計算なので省略。 3. を示す。2. より
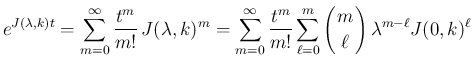
 では
では
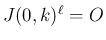 なので、
なので、
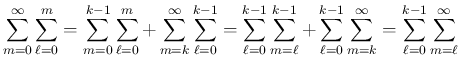
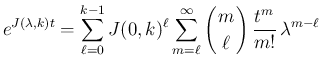
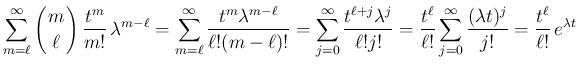
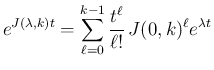
この定理 6.1 により、 ジョルダン標準形 (12) に対し、
![$\displaystyle e^{Jt}=\left[\begin{array}{ccc}e^{J(\lambda_1,k_1)t} & \multicolu...
...umn{2}{l}{\raisebox{0ex}{\LARGE$0$}} & e^{J(\lambda_s,k_s)t}\end{array}\right]
$](img235.png)
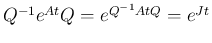 なので、
と求まることになる。
これが通常の
なので、
と求まることになる。
これが通常の 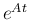 (や
(や 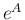 ) の計算方法である。
) の計算方法である。
ただし、次数が大きなジョルダン標準形の計算にはそれなりの手間がかかるし、
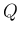 から
から 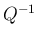 を求めるのも簡単ではない。
だから、この方法での
を求めるのも簡単ではない。
だから、この方法での 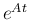 の計算は、
手計算では
の計算は、
手計算では 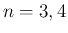 あたりが限界だろう。
なお、もちろん
あたりが限界だろう。
なお、もちろん 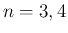 でも固有値が簡単に求まるとは限らないから、
手計算が常に可能であるとの保証はない。
でも固有値が簡単に求まるとは限らないから、
手計算が常に可能であるとの保証はない。
あとで一つ例を紹介する。
竹野茂治@新潟工科大学