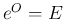
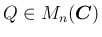 が正則ならば、
が正則ならば、
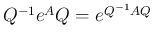
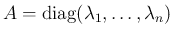 に対して
に対して
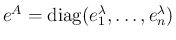 、より一般に、
三角行列
、より一般に、
三角行列
![$\displaystyle A = \left[\begin{array}{ccc}\lambda_1 & \multicolumn{2}{r}{\raise...
...}{l}{\raisebox{.5ex}{\hspace{.3em}\Huge$\ast$}} & \lambda_n\end{array}\right]
$](img103.png)
![$\displaystyle e^A = \left[\begin{array}{ccc}e^{\lambda_1} & \multicolumn{2}{r}{...
...\raisebox{.5ex}{\hspace{.3em}\Huge$\ast$}} & e^{\lambda_n}\end{array}\right]
$](img104.png)
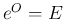
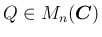 が正則ならば、
が正則ならば、
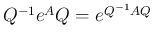
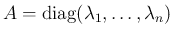 に対して
に対して
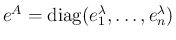 、より一般に、
三角行列
、より一般に、
三角行列
![$\displaystyle A = \left[\begin{array}{ccc}\lambda_1 & \multicolumn{2}{r}{\raise...
...}{l}{\raisebox{.5ex}{\hspace{.3em}\Huge$\ast$}} & \lambda_n\end{array}\right]
$](img103.png)
![$\displaystyle e^A = \left[\begin{array}{ccc}e^{\lambda_1} & \multicolumn{2}{r}{...
...\raisebox{.5ex}{\hspace{.3em}\Huge$\ast$}} & e^{\lambda_n}\end{array}\right]
$](img104.png)
1. 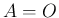 なら (1) の最初の項以外は
なら (1) の最初の項以外は 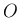 なので明らか。
なので明らか。
2. 部分和に対して
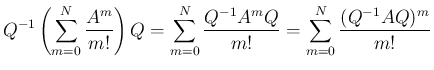
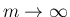 とすれば成立する。
とすれば成立する。
3. 三角行列 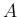 ,
, 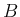 に対して
に対して
![$\displaystyle A^m = \left[\begin{array}{ccc}\lambda_1^m & \multicolumn{2}{r}{\r...
...l}{\raisebox{.5ex}{\hspace{.3em}\Huge$\ast$}} & \lambda_n^m\end{array}\right]
$](img107.png)
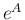 ,
, 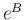 の対角成分は、いずれも
の対角成分は、いずれも
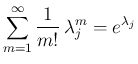
よって、 次正方行列
次正方行列 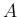 が対角化できる場合には、
行列乗
が対角化できる場合には、
行列乗 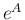 も容易に計算できるが、
対角化できない行列の場合は、一般には後で説明するジョルダン標準形による
計算を行う。
も容易に計算できるが、
対角化できない行列の場合は、一般には後で説明するジョルダン標準形による
計算を行う。
なお、スペクトル分解 (
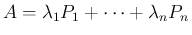 ) できるような
行列であれば、
それを元に行列乗を計算することも可能だが、
そのような行列は対角化も可能なので、
スペクトル分解による計算と対角化での計算ではさほどの優劣はないだろう。
) できるような
行列であれば、
それを元に行列乗を計算することも可能だが、
そのような行列は対角化も可能なので、
スペクトル分解による計算と対角化での計算ではさほどの優劣はないだろう。
証明
(1) の部分和を 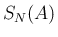 で表すことにする。
で表すことにする。
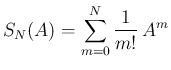
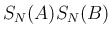 を
を
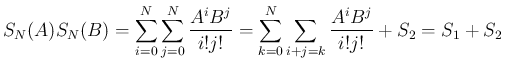
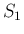 は
は 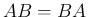 より、
より、
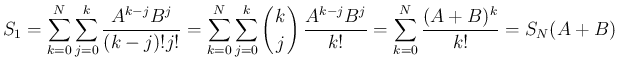
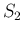 は、
は、
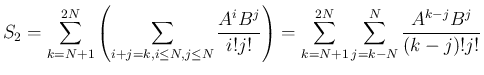
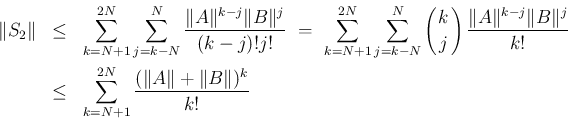
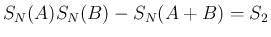 で
で
 と
すれば
と
すれば
 より
より
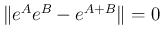 となる。
となる。
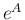 は常に正則で、
は常に正則で、
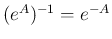
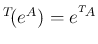
1. 定理 4.2 より、
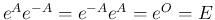 と
なる。
と
なる。
2. 部分和に対して、
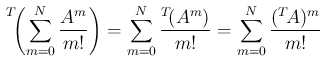
 とすれば得られる。
とすれば得られる。
竹野茂治@新潟工科大学