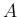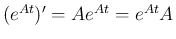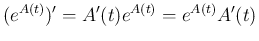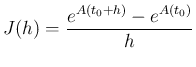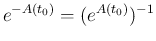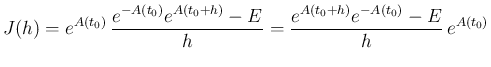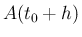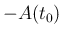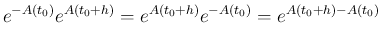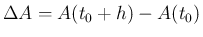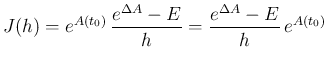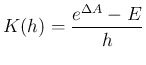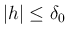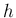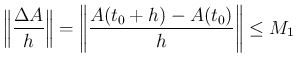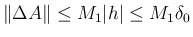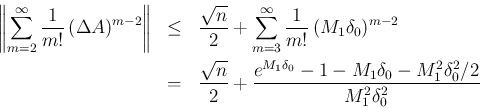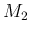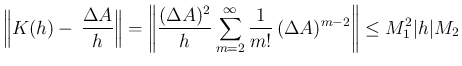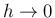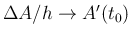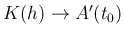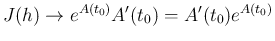5 行列値関数と導関数
本節の内容は、行列が正方行列である必要はない。
定義 5.1
- 成分が実数変数
 の関数
の関数 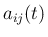 (関数値は実数でも
複素数でも構わない) である行列
(関数値は実数でも
複素数でも構わない) である行列
![$A(t)=[a_{ij}(t)]_{i,j}$](img131.png) を行列値関数と呼ぶ。
を行列値関数と呼ぶ。
- 行列値関数
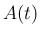 に対し、
極限
に対し、
極限
![$\displaystyle \lim_{t\rightarrow t_0}{A(t)}=B\ (=[b_{ij}]_{i,j})$](img133.png) を、
を、
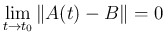 で定義する。
これは、すべての成分に対し
で定義する。
これは、すべての成分に対し
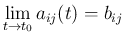 となることと同値である。
となることと同値である。
- 行列値関数
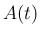 が
が 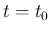 で連続であるとは、
で連続であるとは、
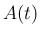 が
が 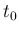 の近傍で定義され、
かつ
の近傍で定義され、
かつ
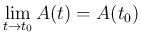 を満たすこととする。
これは、すべての成分が
を満たすこととする。
これは、すべての成分が 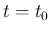 で連続であることと同値である。
で連続であることと同値である。
これは通常の 1 変数関数と同様の定義であるが、区間での連続性や、
半連続性なども通常の 1 変数関数と同様に定義する。
- 行列値関数
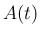 が
が 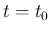 で微分可能であるとは、
で微分可能であるとは、
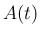 が
が 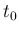 の近傍で定義され、
かつ極限 (微分係数)
が存在することを意味する。
これは、すべての成分が
の近傍で定義され、
かつ極限 (微分係数)
が存在することを意味する。
これは、すべての成分が 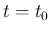 で微分可能であることと同値であり、
で微分可能であることと同値であり、
![$A'(t_0)=[a_{ij}'(t_0)]_{i,j}$](img140.png) となる。
となる。
高階導関数や 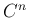 性 (
性 (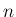 階連続微分可能性) なども
通常の 1 変数関数と同様に定義する。
階連続微分可能性) なども
通常の 1 変数関数と同様に定義する。
定理 5.2
行列の導関数について次が成り立つ。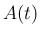 ,
, 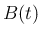 等は微分可能な行列値関数、
等は微分可能な行列値関数、
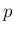 ,
, 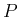 はそれぞれ定数値、定数行列とし、行列の和や積などは
それらが計算できる場合に成立するものとする。
はそれぞれ定数値、定数行列とし、行列の和や積などは
それらが計算できる場合に成立するものとする。
-
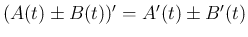
-
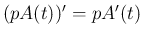 ,
,
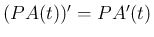 ,
,
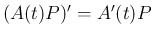
-
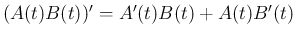
-
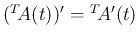
-
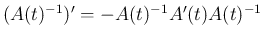
- 区間
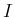 内のすべての
内のすべての 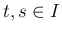 に対して
に対して 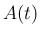 と
と 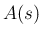 が可換であれば、
が可換であれば、
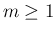 に対して
に対して 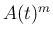 と
と 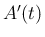 は可換。
は可換。
- 区間
 内のすべての
内のすべての 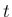 で
で 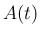 が正則で、
が正則で、
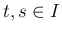 に対して
に対して 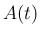 と
と 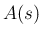 が可換であれば、
が可換であれば、
 に対して
に対して  と
と 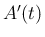 はそれぞれ可換。
はそれぞれ可換。
証明
1., 2., 3., 4., は易しいので (成分を考えれば明らか) 省略。
5. 以降を示す。
5.
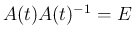 の両辺を
の両辺を 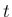 で微分すれば、3. により
で微分すれば、3. により
となるので、両辺左から 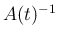 倍すれば得られる。
倍すれば得られる。
6.
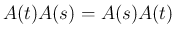 であれば、両辺を
であれば、両辺を 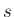 で微分して
で微分して 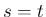 とすれば
とすれば
となり、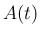 と
と 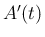 は可換になる。
よって、容易に
は可換になる。
よって、容易に
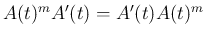 が得られる。
が得られる。
7.
6. により
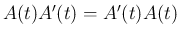 が成り立つので、
この両辺に左からと右から
が成り立つので、
この両辺に左からと右から 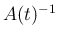 をかければ、
をかければ、
となり、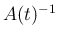 と
と 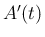 は可換になるので、
容易に
は可換になるので、
容易に
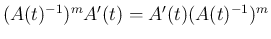 が得られる。
が得られる。
なお、一般には 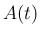 と
と 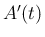 は可換ではない。例えば、
は可換ではない。例えば、
の場合、
となるので可換ではない。
定理 5.3
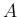 が定数行列の場合、
が定数行列の場合、
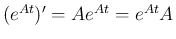
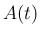 が区間
が区間 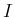 内で微分可能で、すべての
内で微分可能で、すべての 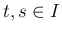 に対して
に対して 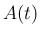 と
と 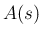 が可換であれば、
が可換であれば、
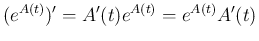
証明
2. のみを示せばよい。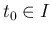 に対して
に対して
とすると、
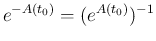 より
となるが、仮定より
より
となるが、仮定より 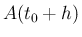 と
と 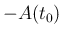 は可換なので
定理 4.2 より
となるので、
は可換なので
定理 4.2 より
となるので、
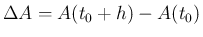 とすれば、
とすれば、
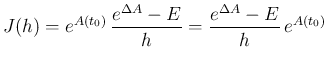 (11)
(11)
となる。今、
とすると、
と書ける。ここで、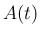 の微分可能性により、
ある
の微分可能性により、
ある 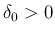 ,
, 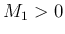 が取れて、
が取れて、
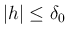 である
任意の
である
任意の 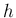 に対して
とできる。よって、
に対して
とできる。よって、
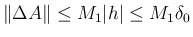 となるので、
となる。よって、この最後の右辺を
となるので、
となる。よって、この最後の右辺を 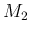 とすれば、
となるので、これは
とすれば、
となるので、これは
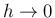 のときに 0 に収束する。
また、
のときに 0 に収束する。
また、
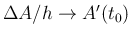 となるので、
よって
となるので、
よって
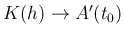 となることがわかる。
となることがわかる。
結局、(11) より、
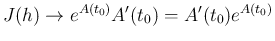 となる。
となる。
竹野茂治@新潟工科大学
2022-05-02
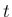 の関数
の関数 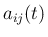 (関数値は実数でも
複素数でも構わない) である行列
(関数値は実数でも
複素数でも構わない) である行列
![$A(t)=[a_{ij}(t)]_{i,j}$](img131.png) を行列値関数と呼ぶ。
を行列値関数と呼ぶ。
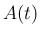 に対し、
極限
に対し、
極限
![$\displaystyle \lim_{t\rightarrow t_0}{A(t)}=B\ (=[b_{ij}]_{i,j})$](img133.png) を、
を、
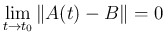 で定義する。
これは、すべての成分に対し
で定義する。
これは、すべての成分に対し
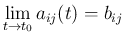 となることと同値である。
となることと同値である。
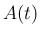 が
が 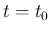 で連続であるとは、
で連続であるとは、
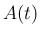 が
が 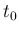 の近傍で定義され、
かつ
の近傍で定義され、
かつ
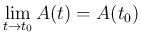 を満たすこととする。
これは、すべての成分が
を満たすこととする。
これは、すべての成分が 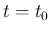 で連続であることと同値である。
で連続であることと同値である。
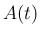 が
が 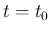 で微分可能であるとは、
で微分可能であるとは、
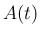 が
が 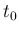 の近傍で定義され、
かつ極限 (微分係数)
の近傍で定義され、
かつ極限 (微分係数)
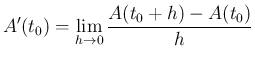
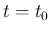 で微分可能であることと同値であり、
で微分可能であることと同値であり、
![$A'(t_0)=[a_{ij}'(t_0)]_{i,j}$](img140.png) となる。
となる。
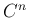 性 (
性 (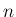 階連続微分可能性) なども
通常の 1 変数関数と同様に定義する。
階連続微分可能性) なども
通常の 1 変数関数と同様に定義する。
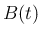
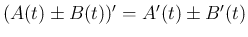
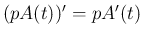
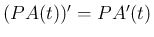
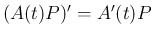
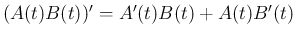
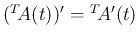
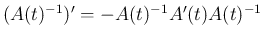
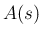
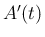
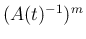
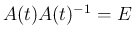
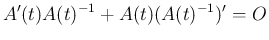
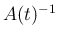
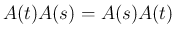
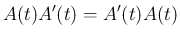
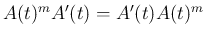
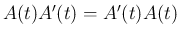
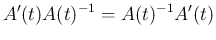
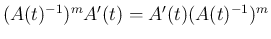
![$\displaystyle A(t)=\left[\begin{array}{cc}t & \sin t\\ 0 & 1\end{array}\right]
$](img169.png)
![$\displaystyle A'(t)=\left[\begin{array}{cc}1 & \cos t\\ 0 & 0\end{array}\right]...
...e{1zw}
A'A=\left[\begin{array}{cc}t & \sin t +\cos t\\ 0 & 0\end{array}\right]
$](img170.png)