行列式を ![]() 列目で展開すると、
列目で展開すると、
(9)
(10)
この展開公式の証明も、帰納法で得ることができる。 なお、行に関する展開公式 (10) は、 列に関する展開公式 (9) と 転置行列に対する定理 2 を組み合わせれば 容易に得られるので、ここでは (9) のみを考える。
(9) はもちろん ![]() の場合には明らかに成り立つので、
の場合には明らかに成り立つので、
![]() 次では任意の列の展開が可能だとして、
(9) を示すこととする。
なお、
次では任意の列の展開が可能だとして、
(9) を示すこととする。
なお、![]() のときは行列式の定義 (1) そのものなので、
のときは行列式の定義 (1) そのものなので、
![]() の場合を考える。
の場合を考える。
このとき ![]() を 1 列目に関して展開すると、
を 1 列目に関して展開すると、
![]() の 1 列目は、
の 1 列目は、![]() の 1 列目の
の 1 列目の ![]() 行目以外の成分なので、
行目以外の成分なので、
(11)
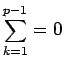 ,
,
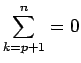 と考えることとする。
と考えることとする。
これを、(9) の右辺に代入すると、
ここで、![]() 次の行列式である
次の行列式である ![]() は、
帰納法の仮定により
は、
帰納法の仮定により ![]() 列目で展開できるが、
列目で展開できるが、
![]() の
の ![]() 列目は
列目は
![]() の
の ![]() 列目の
列目の ![]() 行目以外の成分なので、よって、
行目以外の成分なので、よって、
また、(9), (10) より、
![]() は各列の成分 (または各行の成分) の 1 次式であることが言えるので、
よって、次のことも言える。
は各列の成分 (または各行の成分) の 1 次式であることが言えるので、
よって、次のことも言える。
![]() は各列 (または各行) に関して線形である。
すなわち、ある列が
は各列 (または各行) に関して線形である。
すなわち、ある列が ![]() 倍されれば行列式の値は
倍されれば行列式の値は ![]() 倍となり、
ある列が 2 つの列ベクトルの和であれば、
それぞれをその列とした行列式の和になり、
さらにある列の要素がすべて 0 であれば行列式の値は 0 となる。
倍となり、
ある列が 2 つの列ベクトルの和であれば、
それぞれをその列とした行列式の和になり、
さらにある列の要素がすべて 0 であれば行列式の値は 0 となる。
これにより、行列式を ![]() 個の列ベクトルの関数と見た場合、
そのそれぞれに関して線形である、ということになるので、
これを 多重線形性 と呼ぶことがある。
個の列ベクトルの関数と見た場合、
そのそれぞれに関して線形である、ということになるので、
これを 多重線形性 と呼ぶことがある。
竹野茂治@新潟工科大学