3 転置行列
定理 2
転置行列 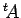 に対して、
に対して、
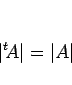 |
(4) |
この定理の証明は、次のように帰納法を使って証明される。
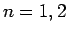 のときは明らかに成立する。
よって、
のときは明らかに成立する。
よって、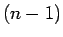 次、
次、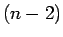 次に対しては成り立つとして、
次に対しては成り立つとして、
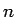 次の場合に成り立つことを証明する
次の場合に成り立つことを証明する 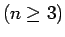 。
。
定義 (1) より、
![\begin{displaymath}
\vert{}^t\!A\vert
=
\vert[a_{ji}]\vert
=
\sum_{p=1}^n(-1)^{p...
...=
a_{11}\Delta_{11}({}^t\!A)-a_{12}\Delta_{21}({}^t\!A)+\cdots
\end{displaymath}](img21.gif)
となるが、
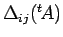 は
は
「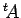 から
から 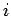 行目、
行目、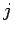 列目を取り除いた行列の行列式」
列目を取り除いた行列の行列式」
なので、よって
「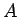 から
から 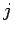 行目、
行目、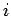 列目を取り除いた行列を転置したものの行列式」
列目を取り除いた行列を転置したものの行列式」
となり、これは 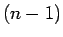 次の行列式であるから、
帰納法の仮定により、転置したものの行列式は転置する前の行列の行列式に等しい。
よって、
次の行列式であるから、
帰納法の仮定により、転置したものの行列式は転置する前の行列の行列式に等しい。
よって、
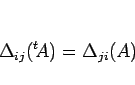 |
(5) |
となることが言える。
よって、
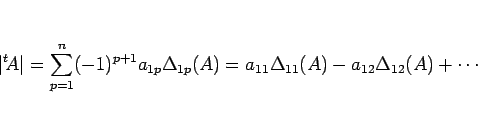 |
(6) |
となる1。
この (6) の 2 番目以降の
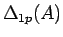 (
(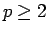 )
は、
)
は、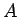 の 1 行目と
の 1 行目と 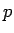 列目を取り除いた行列式であり、
その行列式の 1 列目は、
列目を取り除いた行列式であり、
その行列式の 1 列目は、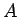 の 1 列目の 2 行目以下の成分に等しい。
の 1 列目の 2 行目以下の成分に等しい。
よって、
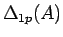 を 1 列目で展開すると、
を 1 列目で展開すると、
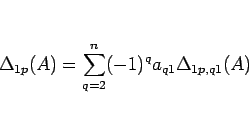 |
(7) |
となる。ここで、
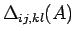 は、
は、
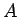 から
から 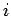 行目と
行目と 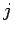 列目、
および (
列目、
および (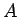 の)
の) 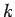 行目と
行目と 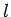 列目を取り除いた
列目を取り除いた 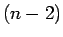 次の行列式を
表すものとする。
次の行列式を
表すものとする。
一方で 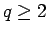 に対し (5) より
に対し (5) より
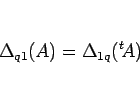
であり、この右辺の行列式を 1 列目で展開すれば、
これは (6) で見たように
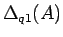 を 1 行目で展開した式となるが、
を 1 行目で展開した式となるが、
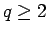 より
より
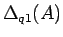 の 1 行目は
の 1 行目は 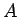 の 1 行目の
2 列目以降の成分に等しいので、
の 1 行目の
2 列目以降の成分に等しいので、
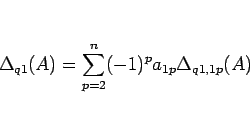 |
(8) |
となる。
明らかに
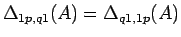 であるので
よって、(6), (7), (8)
と行列式の定義より、
であるので
よって、(6), (7), (8)
と行列式の定義より、
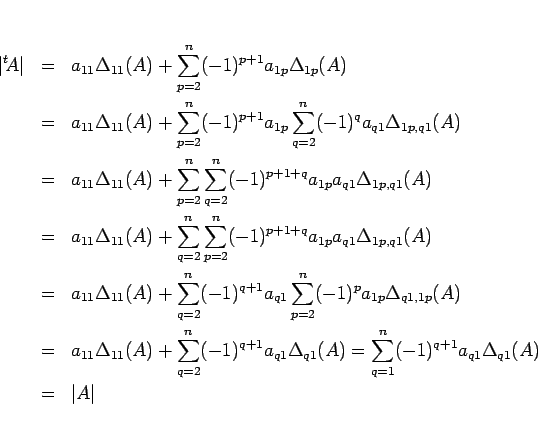
となる。
竹野茂治@新潟工科大学
2006年12月8日
![]() に対して、
に対して、
![]() のときは明らかに成立する。
よって、
のときは明らかに成立する。
よって、![]() 次、
次、![]() 次に対しては成り立つとして、
次に対しては成り立つとして、
![]() 次の場合に成り立つことを証明する
次の場合に成り立つことを証明する ![]() 。
。
から
行目、
列目を取り除いた行列の行列式」
から
行目、
列目を取り除いた行列を転置したものの行列式」
![]() を 1 列目で展開すると、
を 1 列目で展開すると、
![]() に対し (5) より
に対し (5) より
![]() であるので
よって、(6), (7), (8)
と行列式の定義より、
であるので
よって、(6), (7), (8)
と行列式の定義より、