5 導関数
次は、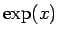 の導関数を考える。
そのために、まず
の導関数を考える。
そのために、まず
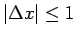 となる
となる 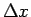 に対して、
に対して、
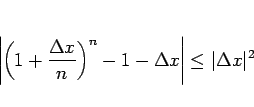 |
(31) |
の不等式が成り立つことを示す。
なので、
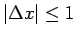 のときは (8) より、
のときは (8) より、
となり、(31) が成り立つことがわかる。
この式で
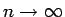 の極限を考えると、
の極限を考えると、
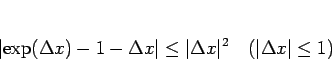 |
(32) |
が得られる。指数法則により
となるから、よって (32) より、
となるので、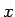 を固定して
を固定して
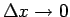 とすれば、
右辺は 0 に収束するから、
とすれば、
右辺は 0 に収束するから、
となり、これは 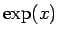 の導関数が
の導関数が 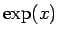 であること
であること
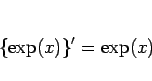 |
(33) |
を意味する。
なお、逆関数の微分公式
を用いれば、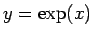 の逆関数
の逆関数 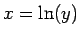 の導関数は、
の導関数は、
となるので、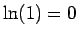 より、
より、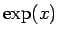 の逆関数
の逆関数 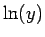 は、
いわゆるメルカトルの自然対数 (双曲対数)
は、
いわゆるメルカトルの自然対数 (双曲対数)
に等しいことがわかる。
竹野茂治@新潟工科大学
2017年2月2日