(yex)' = 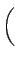
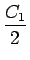 e2x
e2x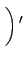
「2 回微分して元に戻るものは、 y = C1ex + C2e-x の形の式のみ」
この問題は、2 階の (定数係数線形の) 微分方程式
を解けばいいわけであるが、 ここでは、標準的な定数係数線形微分方程式の解法、 およびその理論は用いず、 (4) から直接
y'' = y (4)
を導くいくつかの方法を紹介する。
y = C1ex + C2e-x (5)
(4) の両辺に y' を加えると、
となるが、左辺は (y' + y)' であるから、z = y' + y とすれば、これは
y'' + y' = y' + y
を意味する。 2, 3 節の結果により これは z = C1ez を意味するので、よって、
z' = z
が得られる。
y' + y = C1ex (6)
この (6) を、 1 階線形微分方程式の解法と同様の変形をしてみよう。 (6) の両辺を ex 倍すると、
となるが、この左辺は y'ex + y(ex)' = (yex)' に等しい。 (e2x)' = 2e2x なので、この両辺は、
y'ex + yex = C1e2x
と変形できる。よって
(yex)' =e2x
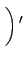
となるので、(3) によりこのかっこの中味が定数となり、
yex -
e2x
= 0
となる。よってこの両辺を ex で割れば
yex =e2x + C2
となり、(5) が得られることになる。
y =e2x +
=
ex + C2e-x
ただ、これはいかにも少し作為的にも見えるが、 (6) を微分方程式として解くのではなく、 もう一本同等のものを導いて利用する、という方法もある。
(4) の両辺から y' を引くと、
となるので、w = y' - y とすれば、これは w' = - w を意味し、 3 節の結果によりここから w = C2e-x 、すなわち
y'' - y' = - y' + y = - (y' - y)
が導かれる。 よって、(6) から (7) を引いて 2 で割れば
y' - y = C2e-x (7)
となり、(5) が得られる。
y =ex -
e-x
この (6), (7) を導く方法は、 微分演算子 D = ' によって (4) を、
のように変形した考察、すなわちいわゆる演算子法と実質的に同等である。
D2y = y, (D2 -1)y = 0, (D + 1)(D - 1)y = 0, (D - 1)(D + 1)y = 0
竹野茂治@新潟工科大学