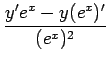 =
= 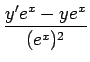 =
= 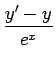
となるが、y が (1) を満たしていればこの式は 0 になる。 なお、商の微分を使う代わりに、積に直して、
=
=
=
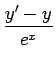
とする方法もある。
= (ye-x)' = y'e-x + y(e-x)' = y'e-x + y(- e-x) = (y' - y)e-x
いずれにせよ、導関数が 0 になるので、 (3) により y/ex が定数となり、 よって (2) が得られることになる。
この方法の方が 2 節の方法よりもシンプルであるし、 例えば次のように発展したもの:
「微分したものが元の関数の定数倍、すなわち y' = ay となるものは何か」もこの方法ならばすぐに解ける。
(eax)' = aeax であるので、 その解は y = Ceax であることが想像されるが、
となるので、確かに y/eax = C となり、 y = Ceax が言える。
= (ye-ax)' = y'e-ax + y(- ae-ax) = (y' - ay)e-ax = 0
竹野茂治@新潟工科大学