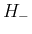
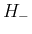 の
の
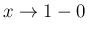 に対する評価を行う。
本節では
に対する評価を行う。
本節では
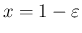 とおいて、
とおいて、
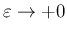 を考える。
この場合、
を考える。
この場合、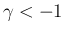 の拡張に関しても考察する必要がある。
の拡張に関しても考察する必要がある。
まずは 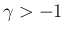 の場合を考える。この場合は、
補題 3 と前節の評価 (40) を
用いればよい。
まず、補題 3 より、
の場合を考える。この場合は、
補題 3 と前節の評価 (40) を
用いればよい。
まず、補題 3 より、
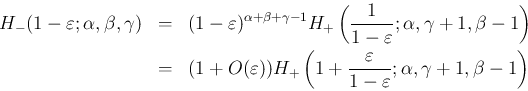
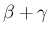 が小さくなるにつれ悪くなる (大きくなる) ことに注意する。
が小さくなるにつれ悪くなる (大きくなる) ことに注意する。
次は 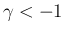 の場合を考える。まず、
の場合を考える。まず、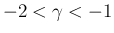 とする。
とする。
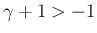 なので、この右辺に
既知の評価 (41) を適用すれば、
なので、この右辺に
既知の評価 (41) を適用すれば、
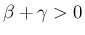 の場合は (42) の右辺は
の場合は (42) の右辺は
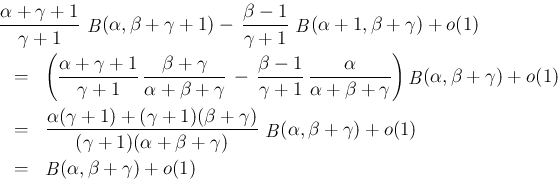
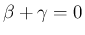 のときは (42) の右辺の前者の項は有界、
後者の項は対数オーダーとなるので、
のときは (42) の右辺の前者の項は有界、
後者の項は対数オーダーとなるので、
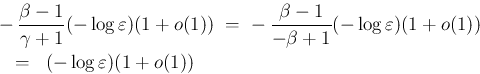
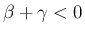 のときも後者の項の方が評価が悪いので、
のときも後者の項の方が評価が悪いので、
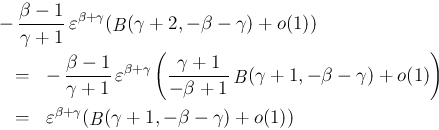
これで 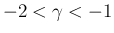 の場合に (41) が成立することが
示されたことになる。
の場合に (41) が成立することが
示されたことになる。
一方で、この証明では 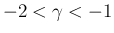 であることは実質的には用いておらず、
よって
であることは実質的には用いておらず、
よって 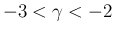 の場合も、
の場合も、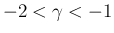 で (41) が成立することを利用して、上と全く同じ計算により証明を行うことができる。
つまり、すべての
で (41) が成立することを利用して、上と全く同じ計算により証明を行うことができる。
つまり、すべての 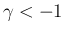 の場合に対して (41) が成り立つことを帰納的に証明することができるので、
これで (41) が
の場合に対して (41) が成り立つことを帰納的に証明することができるので、
これで (41) が 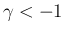 の場合も成立することが
示されたことになる。
の場合も成立することが
示されたことになる。
なお、
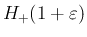 の評価 (40) と、
の評価 (40) と、
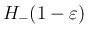 の評価 (41) を比較すると、
よく似た形で、
の評価 (41) を比較すると、
よく似た形で、
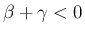 の場合の係数に少しだけ違いがあることが
わかる。
の場合の係数に少しだけ違いがあることが
わかる。
竹野茂治@新潟工科大学