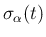
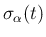 が
が 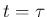 で他の front
で他の front 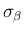 と衝突するとし、
このとき、
を示す。
まず、
と衝突するとし、
このとき、
を示す。
まず、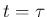 の前後で
の前後で
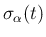 の符号は変わらずに
正のままなので、
の符号は変わらずに
正のままなので、
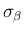 以外の項は
以外の項は
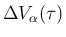 には現れず、
よって (32) の 1 つ目は正しい。
(32) の 2 つ目は、
(7), (11), (23) より、
には現れず、
よって (32) の 1 つ目は正しい。
(32) の 2 つ目は、
(7), (11), (23) より、
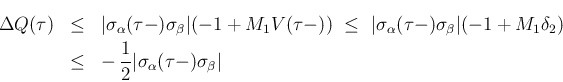
(32) の 3 つ目は、[A-1] の場合は Lemma 7.2 (i) より、
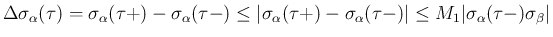
[A-2] の場合は
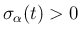 より
より
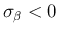 で、
よって Lemma 7.2 (ii) より、
で、
よって Lemma 7.2 (ii) より、
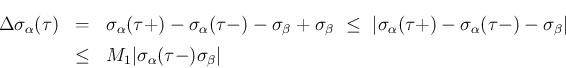
[S-1], [S-3] の場合は
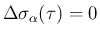 で、
[S-2] の場合は
で、
[S-2] の場合は
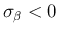 で、
よって
で、
よって
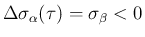 となるから、
よってすべての場合で (32) の 3 つ目が成り立つことがわかる。
となるから、
よってすべての場合で (32) の 3 つ目が成り立つことがわかる。
これで、(32) がすべて成り立つことになる。
今、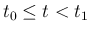 に対して
に対して
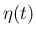 は定数で、
衝突点
は定数で、
衝突点 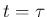 で CASE 1 なら (26) より、
となるし、CASE 2 なら (32)、
および
で CASE 1 なら (26) より、
となるし、CASE 2 なら (32)、
および
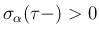 より、
となるので、
より、
となるので、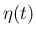 は非増加であることがわかり、よって (21), (23), (24) より、
となり、よって、
が得られる。
は非増加であることがわかり、よって (21), (23), (24) より、
となり、よって、
が得られる。
この (37) は [1] の (7.61) (p138) に
対応するが、これは、定義 7.1 (p125) の 3. (7.8) の、膨張 front の
サイズ 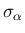 が
が
![$\displaystyle \sigma_\alpha\in]0,\varepsilon]
$](img307.png)
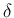 を小さく変更すれば、
もちろんそれに伴い近似解の構造もだいぶ変わってしまうが、
それとは無関係に (37) は常に成立するので、
よって、
を小さく変更すれば、
もちろんそれに伴い近似解の構造もだいぶ変わってしまうが、
それとは無関係に (37) は常に成立するので、
よって、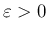 に対して、
に対して、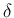 を
となるようにとれば確かに (7.8) が満たされる。
それは、定理 7.2 (p127) の一部でもあるが、
それについてはまた後 (5.9 節) で説明する。
を
となるようにとれば確かに (7.8) が満たされる。
それは、定理 7.2 (p127) の一部でもあるが、
それについてはまた後 (5.9 節) で説明する。
竹野茂治@新潟工科大学