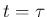 では
では 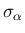 が衝突せず、
が衝突せず、
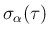 とは別のところで
とは別のところで 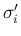 ,
, 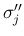 が
衝突して
が
衝突して 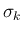 が生成するとする (Riemann 問題の解は
が生成するとする (Riemann 問題の解は
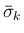 )。
また、
)。
また、
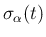 は
は 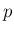 -特性族の膨張 front 接続であるとする。
-特性族の膨張 front 接続であるとする。
この場合、衝突時刻 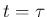 では
では 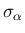 が衝突せず、
が衝突せず、
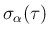 とは別のところで
とは別のところで 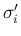 ,
, 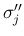 が
衝突して
が
衝突して 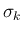 が生成するとする (Riemann 問題の解は
が生成するとする (Riemann 問題の解は
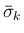 )。
また、
)。
また、
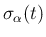 は
は 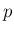 -特性族の膨張 front 接続であるとする。
-特性族の膨張 front 接続であるとする。
示すべきは、
であるが、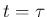 では
では 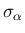 が衝突しないので、当然
が衝突しないので、当然
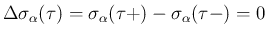
一方、(26) の 2 つ目は自明ではない。
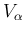 が
が  であれば、(23) の 1 本目より
(26) の 2 つ目は当然成立するが、
であれば、(23) の 1 本目より
(26) の 2 つ目は当然成立するが、
 ではなく
ではなく 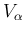 であるため少し詳しく考える必要がある。
まず、以下が成り立つことを場合分けで示す。
であるため少し詳しく考える必要がある。
まず、以下が成り立つことを場合分けで示す。