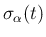
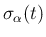 として、
として、
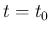 で発生した「rarefaction front」としているが、
これは本稿の「front 接続」を指している。
で発生した「rarefaction front」としているが、
これは本稿の「front 接続」を指している。
また、「rarefaction front」と呼んでいるが、
膨張 front からの front 接続がずっと膨張 front でつながるわけではない。
例えば、[A-1] の場合は、
3.5 節の (5) より
流入 front と同じ特性族に出る front の符号は同じになり、
膨張 front は膨張 front につながるが、
[A-2] の場合は、3.6 節で見たように、
同じ特性族の接触不連続 front 同士、および膨張 front 同士は
衝突しないとしているから、
膨張 front に衝突する他方は衝撃 front となり、
3.6 節の 2. のように
生成する front は
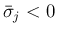 、
すなわち衝撃 front につながることもありうる。
、
すなわち衝撃 front につながることもありうる。
[S-1] の場合も、膨張 front は膨張 front で延長されるが、
[S-2] の場合はやはり衝撃 front との衝突となるので、
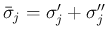 より負になって
衝撃 front につながりうる。
[S-3] の場合は膨張 front は膨張 front のままである。
より負になって
衝撃 front につながりうる。
[S-3] の場合は膨張 front は膨張 front のままである。
この p138 5. の (7.61) の評価は、すべての膨張 front に対して 成り立つことを示すもので、しかもその証明より、 出発点からずっと膨張 front であることが重要である。 よって、むしろ前方に front を延長するよりも、 front 接続を「後方」に膨張 front で延長できるかを考えてみよう。
膨張 front が新たに生成するのは、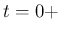 での初期階段関数に対する近似解、
および [A-1]
での初期階段関数に対する近似解、
および [A-1]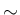 [S-3] のうち、
[A-1] と [A-2] の流入 front とは異なる特性族に発生する膨張 front のみ
であり、それ以外は流入 front と同じ特性族の front のみで、
流入 front 自身に膨張 front が含まれていなければ膨張 front は生成されない。
[S-3] のうち、
[A-1] と [A-2] の流入 front とは異なる特性族に発生する膨張 front のみ
であり、それ以外は流入 front と同じ特性族の front のみで、
流入 front 自身に膨張 front が含まれていなければ膨張 front は生成されない。
これらの新たな膨張 front は、流入 front とは別の特性族なので
要請 (P), (P') の影響は受けず、
よって front の大きさは必ず 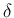 以下であることに注意する。
以下であることに注意する。
次に、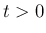 にある膨張 front は、それが新たな膨張 front でなければ、
後方、すなわち
にある膨張 front は、それが新たな膨張 front でなければ、
後方、すなわち 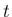 の減る方向には必ず一意に膨張 front につながることを
示そう。
の減る方向には必ず一意に膨張 front につながることを
示そう。
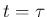 の衝突時刻でその膨張 front が生成され、
かつそれが新たなものでない場合、
の衝突時刻でその膨張 front が生成され、
かつそれが新たなものでない場合、
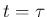 の前後で front の大きさの符号は変わらないので、
後方の front は膨張 front に一意に決まる。
の前後で front の大きさの符号は変わらないので、
後方の front は膨張 front に一意に決まる。
今、そのように後方にのばした膨張 front 接続を
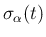 (
(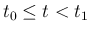 ) と書くことにする。
先の方はわからないが、少なくとも
) と書くことにする。
先の方はわからないが、少なくとも
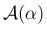 ,
, 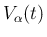 は、
本稿の記号では
を意味する。
は、
本稿の記号では
を意味する。
竹野茂治@新潟工科大学