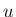
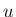 の帰納法による有界変動評価 (7.60) (p138) を示す。
[1] にはごくあっさりと書いてあるが、
ここではもう少し詳しく説明する。
の帰納法による有界変動評価 (7.60) (p138) を示す。
[1] にはごくあっさりと書いてあるが、
ここではもう少し詳しく説明する。
まず、各衝突時刻 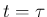 で以下が成り立つことは既に示された。
で以下が成り立つことは既に示された。
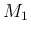 は正の定数で、
考えている
は正の定数で、
考えている 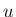 が含まれる領域に依存する。
すなわち、時刻が進むに応じて
が含まれる領域に依存する。
すなわち、時刻が進むに応じて 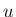 が含まれる領域が広がってしまえば、
これらの定数も大きく取らないといけなくなり、
共通の定数とは取れなくなってしまう可能性があるので、
本来は
が含まれる領域が広がってしまえば、
これらの定数も大きく取らないといけなくなり、
共通の定数とは取れなくなってしまう可能性があるので、
本来は 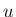 の a priori 評価が得られて
ようやく決定する定数であることに注意しなければいけない。
の a priori 評価が得られて
ようやく決定する定数であることに注意しなければいけない。
ここではそれを帰納法で行うわけであるが、
既知の 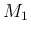 が取れるのは本来は
初期値 (を階段関数で近似した
が取れるのは本来は
初期値 (を階段関数で近似した 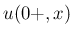 ) に対してのみである。
) に対してのみである。
また、ある定数 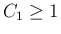 に対して次が成り立つ (p138 (7.59))。
に対して次が成り立つ (p138 (7.59))。
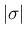 と、その両側の段差
と、その両側の段差 ![$\vert[u]\vert$](img186.png) に
同様の不等式が成り立つことからくるもので、
よってこの
に
同様の不等式が成り立つことからくるもので、
よってこの 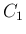 も
も 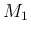 同様
同様 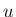 が
含まれる領域に依存する定数である。
が
含まれる領域に依存する定数である。
まず最初の目標は、
が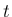 に関して非増加となるような定数
に関して非増加となるような定数 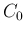 を見つけることである。
を見つけることである。
今、全 front の衝突時刻を小さい方から
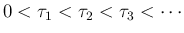
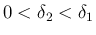 (
(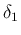 は 7.3 節 の 1. (p133)) を、まず
となるように取る。そして
は 7.3 節 の 1. (p133)) を、まず
となるように取る。そして 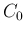 を
となるように取り、
を満たすような
を
となるように取り、
を満たすような 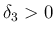 を取る。なお、
を取る。なお、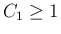 より、
であることに注意する。
(13) を満たす
より、
であることに注意する。
(13) を満たす 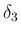 としては、例えば
とでもすればよい。それは、(15) であれば、
としては、例えば
とでもすればよい。それは、(15) であれば、
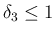 より
より
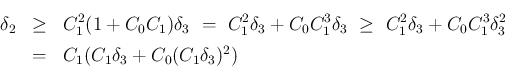
まず、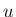 の初期全変動を小さくして、
の初期全変動を小さくして、
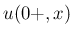 のことを
のことを 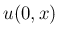 と書いている (p127 (7.17))。
初期値の変動が
と書いている (p127 (7.17))。
初期値の変動が 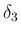 未満であると仮定すれば、
(7.17) より (16) が成り立つようにできる。
となるので、(6), (7) より、
未満であると仮定すれば、
(7.17) より (16) が成り立つようにできる。
となるので、(6), (7) より、
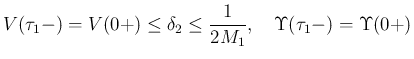
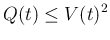
そして、この (22) によって
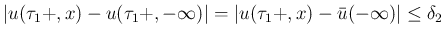
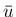 が含まれ、
(6), (7), (8) が
成り立つ
が含まれ、
(6), (7), (8) が
成り立つ 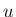 の領域を例えば
の領域を例えば 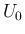 とし、
とし、
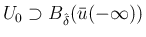
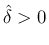 を取り、
を取り、
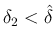 となるように
となるように 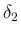 を取れば
を取れば
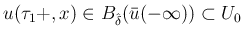
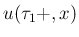 に対しても、同じ
に対しても、同じ 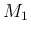 ,
, 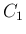 のままで (6), (7), (8) を
使うことができるようになる。
のままで (6), (7), (8) を
使うことができるようになる。
さて、ここからは帰納法により、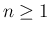 に対して 3 つの不等式
に対して 3 つの不等式
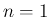 については示された。
については示された。
(23) が 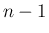 までは成り立つとすると、
上に述べたように、
(23) の 3 本目によりそこまでの
までは成り立つとすると、
上に述べたように、
(23) の 3 本目によりそこまでの 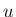 に対しては (6), (7), (8) が
使えて、よって、帰納法の仮定により、
に対しては (6), (7), (8) が
使えて、よって、帰納法の仮定により、
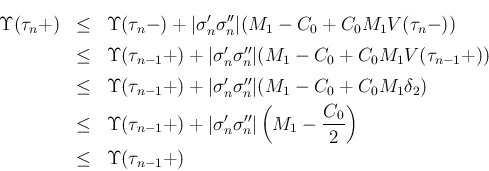
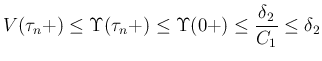
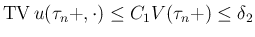
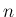 に対して (すなわち近似解が構成できるすべての
に対して (すなわち近似解が構成できるすべての 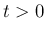 に対して) 成り立つことが言えたことになる。
そして、
に対して) 成り立つことが言えたことになる。
そして、
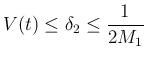
竹野茂治@新潟工科大学